
分析 已知a•b≠1,且有5a2+1997a+8=0及8b2+1997b+5=0,所以a、$\frac{1}{b}$是方程5x2+1997x+8=0的两根,根据根与系数的关系即可求解.
解答 解:由已知5a2+1997a+8=0可得a是方程5x2+1997x+8=0的解,
方程8b2+1997b+5=0,可得$\frac{1}{b}$是方程5x2+1997x+8=0的解,
∴a、$\frac{1}{b}$是方程5x2+1997x+8=0的两根,
由韦达定理可得$\frac{a}{b}$=$\frac{8}{5}$.
点评 此题主要考查了根与系数的关系,得出a、$\frac{1}{b}$是方程5x2+1997x+8=0的两根是解题关键.


科目:初中数学 来源: 题型:解答题
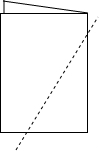 把一张长方形纸对折,任意剪出一个直角边在折线上的直角三角形,把它展开,得到三角形记为△ABC,并将折线的另一端点记为D,如图所示,这是什么特殊三角形?图中有哪些相等的角?有哪些相等的线段?在△ABC中,AD有几种角色?各是什么?
把一张长方形纸对折,任意剪出一个直角边在折线上的直角三角形,把它展开,得到三角形记为△ABC,并将折线的另一端点记为D,如图所示,这是什么特殊三角形?图中有哪些相等的角?有哪些相等的线段?在△ABC中,AD有几种角色?各是什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com