

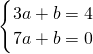 ,
,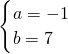 ;
;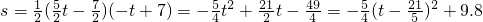 ;
;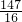
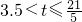 时,有:
时,有: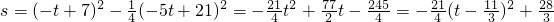 ;
;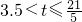 时,s的值小于
时,s的值小于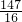 .
.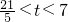 时,有:s=(t-7)2;
时,有:s=(t-7)2;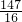 ,
,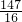 .
.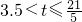 时,此时OD=t,DE=7-t,重合部分的面积可由正方形的面积减去未重合的直角三角形的面积,由此求得S、t的函数关系式;
时,此时OD=t,DE=7-t,重合部分的面积可由正方形的面积减去未重合的直角三角形的面积,由此求得S、t的函数关系式;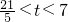 时,此时重合部分的面积就是正方形EFGD的面积,从而求得S、t的函数关系式;
时,此时重合部分的面积就是正方形EFGD的面积,从而求得S、t的函数关系式;

科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 .点T在线段AO上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′,折痕经过点T,折痕TP与射线AB交于点P,设OT=t,折叠后纸片重叠部分(图中的阴影部分)的面积为S.
.点T在线段AO上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′,折痕经过点T,折痕TP与射线AB交于点P,设OT=t,折叠后纸片重叠部分(图中的阴影部分)的面积为S.
查看答案和解析>>
科目:初中数学 来源:2010年江苏省苏州市中考数学模拟试卷(七)(解析版) 题型:解答题
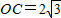 ,点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点OT=t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
,点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点OT=t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;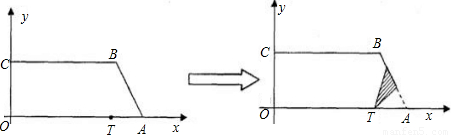
查看答案和解析>>
科目:初中数学 来源:2009年江苏省苏州市高新区中考数学模拟调研统测卷(解析版) 题型:解答题
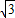 .点T在线段AO上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′,折痕经过点T,折痕TP与射线AB交于点P,设OT=t,折叠后纸片重叠部分(图中的阴影部分)的面积为S.
.点T在线段AO上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′,折痕经过点T,折痕TP与射线AB交于点P,设OT=t,折叠后纸片重叠部分(图中的阴影部分)的面积为S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com