
 ×2b×b=a2+b2,
×2b×b=a2+b2,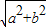 ;
;


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
| h1 | h2 |
 NM与梯形BCNM的重叠面积为S,
NM与梯形BCNM的重叠面积为S,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC.
(2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•深圳)如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是( )
(2013•深圳)如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是( )查看答案和解析>>
科目:初中数学 来源: 题型:
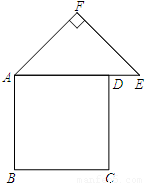
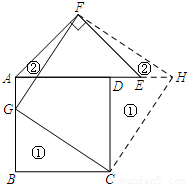
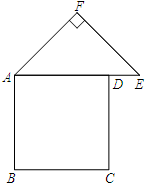 (2012•和平区一模)如图,有一张纸片,是由边长为a的正方形ABCD、斜边长为2b的等腰直角三角形FAE组成的(b<a),∠AFE=90°,且边AD和AE在同一条直线上.要通过适当的剪拼,得到一个与之面积相等的正方形.
(2012•和平区一模)如图,有一张纸片,是由边长为a的正方形ABCD、斜边长为2b的等腰直角三角形FAE组成的(b<a),∠AFE=90°,且边AD和AE在同一条直线上.要通过适当的剪拼,得到一个与之面积相等的正方形.| a2+b2 |
| a2+b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com