
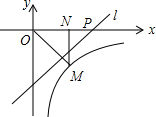
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点M(1,-1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=$\frac{1+\sqrt{5}}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点M(1,-1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=$\frac{1+\sqrt{5}}{2}$. 分析 根据反比例函数图象上点的坐标特征由点A坐标为(1,-1)得到k=-1,即反比例函数解析式为y=-$\frac{1}{x}$,且ON=MN=1,则可判断△OMN为等腰直角三角形,知∠MON=45°,再利用PQ⊥OM可得到∠OPQ=45°,然后轴对称的性质得PN=PN′,NN′⊥PQ,所以∠NPQ=∠N′PQ=45°,于是得到N′P⊥x轴,则点n′的坐标可表示为(t,-$\frac{1}{t}$),于是利用Pn=Pn′得t-1=|-$\frac{1}{t}$|=$\frac{1}{t}$,然后解方程可得到满足条件的t的值.
解答 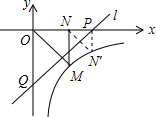 解:如图,∵点M坐标为(1,-1),
解:如图,∵点M坐标为(1,-1),
∴k=-1×1=-1,
∴反比例函数解析式为y=-$\frac{1}{x}$,
∵ON=MN=1,
∴△OMN为等腰直角三角形,
∴∠MON=45°,
∵直线l⊥OM,
∴∠OPQ=45°,
∵点N和点N′关于直线l对称,
∴PN=PN′,NN′⊥PQ,
∴∠N′PQ=∠OPQ=45°,∠N′PN=90°,
∴N′P⊥x轴,
∴点N′的坐标为(t,-$\frac{1}{t}$),
∵PN=PN′,
∴t-1=|-$\frac{1}{t}$|=$\frac{1}{t}$,
整理得t2-t-1=0,解得t1=$\frac{1+\sqrt{5}}{2}$,t2=$\frac{1-\sqrt{5}}{2}$(不符合题意,舍去),
∴t的值为$\frac{1+\sqrt{5}}{2}$.
故答案为:$\frac{1+\sqrt{5}}{2}$.
点评 本题考查了反比例函数的综合题,涉及知识点有反比例函数图象上点的坐标特征、等腰直角三角形的性质和轴对称的性质和用求根公式法解一元二次方程等.利用对称的性质得到关于t的方程是解题的关键.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:选择题
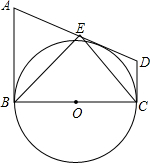 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -2 | -1 | 1 | 2 | 4 | 5 | … |
| y1 | … | -5 | 0 | 4 | 3 | -5 | -12 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
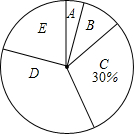 今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:| 分组 | 分数段(分) | 频数 |
| A | 36≤x<41 | 2 |
| B | 41≤x<46 | 5 |
| C | 46≤x<51 | 15 |
| D | 51≤x<56 | m |
| E | 56≤x<61 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com