
在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.

(1)求证:MA=MB;
(2)连接AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
(1)连接OM,由Rt△POQ中,OP=OQ=4,M是PQ的中点可得OM=PM= PQ=2
PQ=2 ,∠POM=∠BOM=∠P=45° ,即得∠PMA=∠OMB,则可证得△PMA≌△OMB,问题得证;(2)存在,4+2
,∠POM=∠BOM=∠P=45° ,即得∠PMA=∠OMB,则可证得△PMA≌△OMB,问题得证;(2)存在,4+2 .
.
【解析】
试题分析:(1)连接OM,由Rt△POQ中,OP=OQ=4,M是PQ的中点可得OM=PM= PQ=2
PQ=2 ,∠POM=∠BOM=∠P=45° ,即得∠PMA=∠OMB,则可证得△PMA≌△OMB,问题得证;
,∠POM=∠BOM=∠P=45° ,即得∠PMA=∠OMB,则可证得△PMA≌△OMB,问题得证;
(2)根据全等三角形的性质可得PA=OB,则OA+OB=OA+PA=OP=4,令OA=x,AB=y,根据勾股定理可得y2=x2+(4-x)2=2x2-8x+16=2(x-2)2+8≥8,再根据二次函数的性质即可作出判断.
(1)连接OM

∵Rt△POQ中,OP=OQ=4,M是PQ的中点
∴OM=PM= PQ=2
PQ=2 ,∠POM=∠BOM=∠P=45°
,∠POM=∠BOM=∠P=45°
∵∠PMA+∠AMO=∠OMB+∠AMO
∴∠PMA=∠OMB,
∴△PMA≌△OMB
∴MA=MB;
(2)△AOB的周长存在最小值
理由是: △PMA≌△OMB
∴PA=OB,∴OA+OB=OA+PA=OP=4
令OA=x,AB=y则y2=x2+(4-x)2=2x2-8x+16=2(x-2)2+8≥8
当x=2时y2有最小值=8从而y≥2
所以⊿AOB的周长存在最小值为4+2 .
.
考点:旋转问题的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
 (2012•南充)在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
(2012•南充)在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:
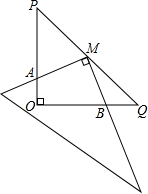 如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.查看答案和解析>>
科目:初中数学 来源:2013届江苏省江阴初级中学九年级上学期期末考试数学试卷(带解析) 题型:填空题
探究:如图,在Rt△POQ中OP=OQ=4,将一把三角尺的直角顶点放在PQ中点M处,以M为旋转中心旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B,连接AB,则△AOB周长的最小值是 .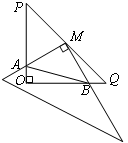
查看答案和解析>>
科目:初中数学 来源:2013届山东省潍坊市九年级复习模拟数学试卷(带解析) 题型:解答题
在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.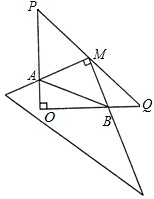
(1)求证:MA=MB;
(2)连接AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com