B
分析:根据题意画出相应的图形,如图所示,由两直角边的长,利用勾股定理求出斜边AC的长,由圆O为三角形的内切圆,得到三角形三边与圆O相切,切点分别为D,E,F,连接圆心与各个切点,根据切线的性质得到OD与AB垂直,OF与BC垂直,又∠B为直角,可得四边形ODBF为矩形,又两半径OD=OF,可得此矩形为正方形,根据正方形的性质得到四条边相等,设出圆的半径为r,根据AD与AE为圆的两条切线,根据切线长定理得到AD=AE=12-r,同理可得出CE=CF=5-r,进而得到AC=AE+EC=AD+CF,列出关于r的方程,求出方程的解可得出r的值.
解答:
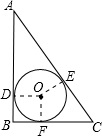
解:∵直角三角形的两直角边长BC=5cm,AC=12cm,
∴根据勾股定理得到直角三角形的斜边AC=
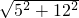
=13cm,
又圆O为三角形的内切圆,D,E,F分别为切点,连接OD,OE,OF,
∴OD⊥AB,OF⊥BC,
∴∠ODB=∠B=∠OFB=90°,
∴四边形OFBD为矩形,又OD=OF,
∴四边形OFBD为正方形,
∴OD=DB=BF=OF,
又AD,AE为圆O的两条切线,
∴AD=AE,
同理CE=CF,BD=BF,
设圆O的半径为rcm,则有BD=BF=rcm,
∴CF=CE=(5-r)cm,AD=AE=(12-r)cm,
又AC=AE+EC=AD+CF=12-r+5-r=17-2r=13,
解得:r=2,
则该直角三角形的内切圆的半径为2cm.
故选B.
点评:此题考查了三角形的内切圆与内心,涉及的知识有:勾股定理,正方形的判定与性质,切线长定理,利用了方程及转化的思想,本题的关键是根据题意画出相应的图形,添加合适的辅助线,设出未知数,建立方程来解决问题.


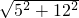 =13cm,
=13cm,

 阅读快车系列答案
阅读快车系列答案 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.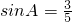 ,其中A为锐角,试求sadA的值;
,其中A为锐角,试求sadA的值;