
【题目】如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.
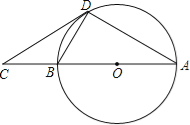
(1)求证:CD是⊙O的切线;
(2)若半径OB=2,求AD的长.
科目:初中数学 来源: 题型:
【题目】为迎接“均衡教育大检查”,县委县府对通往某偏远学校的一段全长为1200 米的道路进行了改造,铺设草油路面.铺设400 米后,为了尽快完成道路改造,后来每天的工作效率比原计划提高25%,结果共用13天完成道路改造任务.
(1)求原计划每天铺设路面多少米;
(2)若承包商原来每天支付工人工资为1500元,提高工作效率后每天支付给工人的工资增长了20%,完成整个工程后承包商共支付工人工资多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c
B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc
D.如果ac=bc,那么a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】衢州市“十二五”规划纲要指出,力争到2015年,全市农民人均年纯收入超13000元,数13000用科学记数法可以表示为( )
A.13×103
B.1.3×104
C.0.13×104
D.130×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为![]() ,当0<x<2时,求y与x的函数关系式;
,当0<x<2时,求y与x的函数关系式;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
已知a,b,c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:因为a2c2-b2c2=a4-b4, ①
所以c2(a2-b2)=( a2-b2)( a2+b2). ②
所以c2= a2+b2. ③
所以△ABC是直角三角形. ④
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的代码为 ;
(2)错误的原因为 ;
(3)请你将正确的解答过程写下来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )

A. 函数有最小值
B. 对称轴是直线x=![]()
C. 当x<![]() ,y随x的增大而减小
,y随x的增大而减小
D. 当﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两车分别从M、N两地相向而行,甲车出发1小时后,乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达N地停止运行,下列说法中正确的是( )

A. M、N两地的路程是1000千米; B. 甲到N地的时间为4.6小时;
C. 甲车的速度是120千米/小时; D. 甲乙两车相遇时乙车行驶了440千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com