


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
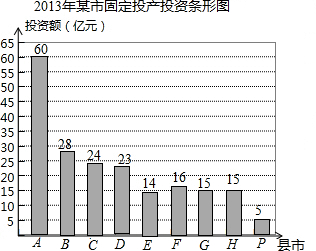 某地统计局对2013年各县市的固定资产投资情况进行了统计,并绘成了如图,请根据相关信息解答下列问题:下列结论不正确的是( )
某地统计局对2013年各县市的固定资产投资情况进行了统计,并绘成了如图,请根据相关信息解答下列问题:下列结论不正确的是( )| A、2013年某市固定资产投资总额为200亿元 |
| B、2013年某市各单位固定资产投资额的中位数是16亿元 |
| C、2013年A县固定资产投资额为占总额的30% |
| D、2013年固定资产投资扇形统计图中表示A地的扇形的圆心角为110° |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
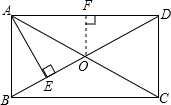 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com