
如图,已知AB是⊙O的直径,PB为⊙O的切线,B为切点,OP⊥弦BC于点D且交⊙O于点E.
(1)求证:∠OPB=∠AEC;
(2)若点C为半圆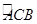 的三等分点,请你判断四边形AOEC为哪种特殊四边形?并说明理由.
的三等分点,请你判断四边形AOEC为哪种特殊四边形?并说明理由.
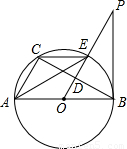
(1)证明:∵AB是⊙O的直径,PB为⊙O的切线,
∴PB⊥AB.
∴∠OPB+∠POB=90°.
∵OP⊥BC,
∴∠ABC+∠POB=90°.
∴∠ABC=∠OPB.
又∵∠AEC=∠ABC,
∴∠OPB=∠AEC.
(2)解:四边形AOEC是菱形.
∵OP⊥弦BC于点D且交⊙O于点E,∴ =
= .
.
∵C为半圆ACB¯的三等分点,∴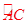 =
= =
= .
.
∴∠ABC=∠ECB.∴AB∥CE.
∵AB是⊙O的直径,∴AC⊥BC.
又 OP⊥弦BC于点D且交⊙O于点E,
∴AC∥OE.∴四边形AOEC是平行四边形.
又 OA=OE,∴四边形AOEC是菱形.
【解析】(1)找中间量∠ABC,利用等角的余角相等证∠ABC=∠OPB,同弧所对的圆周角相等即可
(2)利用用一组邻边相等的平行四边形是菱形及两组对边分别平行的四边形是平行四边形即可。


科目:初中数学 来源: 题型:
 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.| BE | AD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.
如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com