
分析 根据正八边形的性质得出AO=BO=CO=10cm,∠AOB=∠BOC=45°,进而得出AC的长,即可得出S四边形AOCB的面积,进而得出答案.
解答 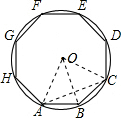 解:连接AO,BO,CO,AC,
解:连接AO,BO,CO,AC,
∵正八边形ABCDEFGH的外接圆O半径为10cm,
∴AO=BO=CO=10cm,∠AOB=∠BOC=$\frac{360°}{8}$=45°,
∴∠AOC=90°,
∴AC=$\sqrt{2}$OA=10$\sqrt{2}$cm,此时AC与BO垂直,
∴S四边形AOCB=$\frac{1}{2}$×BO×AC=$\frac{1}{2}$×10×10$\sqrt{2}$=50$\sqrt{2}$(cm2),
∴正八边形面积为50$\sqrt{2}$×4=200$\sqrt{2}$≈282.8(cm2).
点评 此题主要考查了正多边形和圆的有关计算;根据已知得出中心角∠AOC=90°,再利用勾股定理得出AC是解题关键.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a>0,b>0 | B. | a>0,b<0,|a|>|b| | C. | a<0,b<0 | D. | a<0,b>0,|a|>|b| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
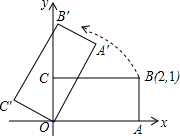 如图在平面直角坐标系中,矩形OABC的一顶点为坐标原点O,边OA、OC分别落在x轴和y轴上,点B的坐标为(2,1);矩形OA′B′C′是由矩形OABC旋转而来的,∠C′OA=150°.
如图在平面直角坐标系中,矩形OABC的一顶点为坐标原点O,边OA、OC分别落在x轴和y轴上,点B的坐标为(2,1);矩形OA′B′C′是由矩形OABC旋转而来的,∠C′OA=150°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5108×106km | B. | 5.010×105km | C. | 5.108×105km | D. | 5.108×106km |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 56×105 | B. | 0.56×106 | C. | 5.6×105 | D. | 5.6×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)(2)(3) | B. | (1)(2)(4) | C. | (2)(3)(4) | D. | (1)(3)(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.88×108元 | B. | 68.8×108元 | C. | 6.88×1010元 | D. | 0.688×1011元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com