
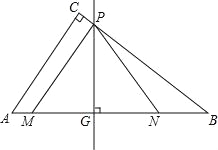
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.
(1)当t= 秒时,动点M、N相遇;
(2)设△PMN的面积为S,求S与t之间的函数关系式.
【答案】(1)2.5
(2)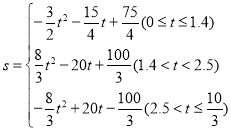
【解析】
试题分析:(1)根据勾股定理可得AB=10,若动点M、N相遇,则有t+3t=10,即可求出t的值;
(2)由于“点P在BC上”与“点P在点AC上”及“点M在点N的左边”与“点M在点N的右边”对应的MN、PG的表达式不同,S与t之间的函数关系式也就不同,因此需分情况讨论.只需先考虑临界位置(点P与点C重合,点M与点N重合、点N与点A重合)所对应的t的值,然后分三种情况(①0≤t≤1.4,②1.4<t<2.5,③2.5<t≤![]() )讨论,用t的代数式表示出MN和PG,就可解决问题.
)讨论,用t的代数式表示出MN和PG,就可解决问题.
试题解析:(1)∵∠ACB=90°,AC=6,BC=8,∴AB=10,
∴t+3t=10,解得t=2.5(s),
即当t=2.5秒时,动点M,N相遇;
故答案为2.5;
(2)过点C作CH⊥AB于H,
由S△ABC=![]() ACBC=
ACBC=![]() ABCH得,CH=
ABCH得,CH=![]() =4.8,
=4.8,
∴AH=![]() =3.6,BH=10﹣3.6=6.4.
=3.6,BH=10﹣3.6=6.4.
∵当点N运动到点A时,M,N两点同时停止运动,∴0≤t≤![]() .
.
当0≤t<2.5时,点M在点N的左边,如图1、图2,
MN=AB﹣AM﹣BN=10﹣t﹣3t=10﹣4t.
∵点G是MN的中点,∴MG=![]() MN=5﹣2t,
MN=5﹣2t,
∴AG=AM+MG=t+5﹣2t=5﹣t,
∴BG=10﹣(5﹣t)=t+5.
当点P与点C重合时,点G与点H重合,
则有5﹣t=3.6,解得t=1.4.
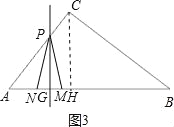
当2.5<t≤![]() 时,点M在点N右边,如图3,
时,点M在点N右边,如图3,
∵MN=AM﹣AN=AM﹣(AB﹣BN)=t﹣(10﹣3t)=4t﹣10,
∴NG=![]() MN=2t﹣5,
MN=2t﹣5,
∴AG=AN+NG=10﹣3t+2t﹣5=5﹣t.
综上所述:①当0≤t≤1.4时,点M在点N的左边,点P在BC上,如图1,
此时MN=10﹣4t,BG=t+5,PG=BGtanB=![]() (t+5)=
(t+5)=![]() t+
t+![]() ,
,
∴S=![]() MNPG=
MNPG=![]() (10﹣4t)(
(10﹣4t)(![]() t+
t+![]() )=﹣
)=﹣![]() t2﹣
t2﹣![]() t+
t+![]() ;
;
②当1.4<t<2.5时,点M在点N的左边,点P在AC上,如图2,
此时MN=10﹣4t,AG=5﹣t,PG=AGtanA=![]() (5﹣t)=
(5﹣t)=![]() ﹣
﹣![]() t,
t,
∴S=![]() MNPG=
MNPG=![]() (10﹣4t)(
(10﹣4t)(![]() ﹣
﹣![]() t)=
t)=![]() t2﹣20t+
t2﹣20t+![]() ;
;
③当2.5<t≤![]() 时,点M在点N的右边,点P在AC上,如图3,
时,点M在点N的右边,点P在AC上,如图3,
此时MN=4t﹣10,AG=5﹣t,PG=AGtanA=![]() (5﹣t)=
(5﹣t)=![]() ﹣
﹣![]() t,
t,
∴S=![]() MNPG=
MNPG=![]() (4t﹣10)(
(4t﹣10)(![]() ﹣
﹣![]() t)=﹣
t)=﹣![]() t2+20t﹣
t2+20t﹣![]() ;
;
∴S与t之间的函数关系式为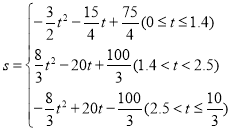 .
.




 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
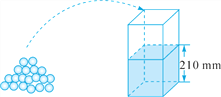
【题目】水平放置的容器内原有210 mm高的水,如图,将若干个球逐一放入该容器中,每放入一个大球水面就上升4 mm,每放入一个小球水面就上升3 mm,假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y(mm).
(1)若只放入大球,且个数为x大,求y关于x大的函数表达式(不必写出x大的取值范围).
(2)若放入6个大球后,开始放入小球,且小球个数为x小.
①求y关于x小的函数表达式(不必写出x小的取值范围).
②若限定水面高不超过260 mm,则最多能放入几个小球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某公司前年缴税40万元,今年缴税48.4万元,求该公司这两年缴税的年平均增长率.设该公司这两年缴税的年平均增长率为x,根据题意,可列方程为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.在农村电网改造中,四个自然村分别位于如图所示的A,B,C,D处,现计划安装一台变压器,使到四个自然村的输电线路的总长最短,那么这个变压器应安装在AC,BD的交点E处,你知道这是为什么吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com