
已知:图1为一锐角是30°的直角三角尺,其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).操作:将三角尺移向直径为4cm的⊙O,它的内Rt△ABC的斜边AB恰好等于⊙O的直径,它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2)。
思考:
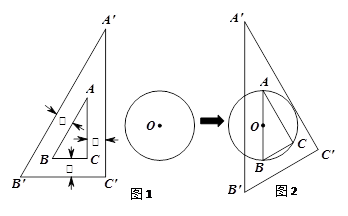
1.求直角三角尺边框的宽
2.求证:![]() BB′C′+
BB′C′+ CC′B′=75°。
CC′B′=75°。
3.求边B′C′的长。
1.过O作OD⊥A′C′于D,交AC于E,

∵AC∥A′C′,
∴AC⊥OD,
∵A′C′与⊙O相切,AB为圆O的直径,且AB=4cm,
∴OD=OA=OB=![]() AB=
AB= ×4=2(cm),
×4=2(cm),
在Rt△AOE中,∠A=30°,
∴OE=![]() OA=
OA= ×2=1(cm),
×2=1(cm),
∴DE=OD-OE=2-1=1(cm)
则三角尺的宽为1cm.(4分
2.∵三角板的宽度是一样大
∴BB′平分∠A′B′C′,C C′平分∠A′C′B′
∵∠A′B′C′=60°,∠A′C′B′=90°
∴![]() BB′C′=30°,
BB′C′=30°,![]() CC′B′=45°
CC′B′=45°
∴![]() BB′C′+
BB′C′+![]() CC′B′=75°(3分)
CC′B′=75°(3分)
3.B′C=![]() .(3分)
.(3分)
解析:(1)OD为圆的半径,利用Rt△AOE中,∠A=30°,算出OE的长,这样就求出DE的长,即为三角尺的宽;
(2)根据三角形的宽度相等得出BB′、CC′是角平分线算出![]() BB′C′、
BB′C′、![]() CC′B′的值,然后证出结论;
CC′B′的值,然后证出结论;
(3)利用三角函数性质计算出B′C的值


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
 ,它的外Rt△A′B′C′的直角边A′C′恰好与⊙O相切(如图2).
,它的外Rt△A′B′C′的直角边A′C′恰好与⊙O相切(如图2).查看答案和解析>>
科目:初中数学 来源:2012届江苏泰兴济川中学九年级中考一模数学试卷(带解析) 题型:解答题
已知:图1为一锐角是30°的直角三角尺,其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).操作:将三角尺移向直径为4cm的⊙O,它的内Rt△ABC的斜边AB恰好等于⊙O的直径,它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2)。
思考:
【小题1】求直角三角尺边框的宽
【小题2】求证: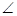 BB′C′+
BB′C′+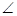 CC′B′=75°。
CC′B′=75°。
【小题3】求边B′C′的长。
查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市六校联谊中考模拟数学试卷(带解析) 题型:解答题
已知:图1为一锐角是30°的直角三角尺,其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).
操作:将三角尺移向直径为4cm的⊙O,它的内Rt△ABC的斜边AB恰好等于⊙O的直径,它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2)。
思考:(1) 求直角三角尺边框的宽。
(2) 求 BB′C′+
BB′C′+ CC′B′的度数。
CC′B′的度数。
(3) 求边B′C′的长。
查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市六校联谊中考模拟数学试卷(解析版) 题型:解答题
已知:图1为一锐角是30°的直角三角尺,其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).
操作:将三角尺移向直径为4cm的⊙O,它的内Rt△ABC的斜边AB恰好等于⊙O的直径,它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2)。

思考:(1) 求直角三角尺边框的宽。
(2) 求 BB′C′+
BB′C′+ CC′B′的度数。
CC′B′的度数。
(3) 求边B′C′的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com