解:(1)(2)所画图形如下所示:
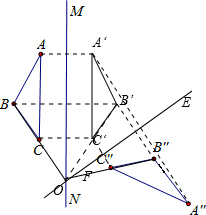
(3)连接B′O.
∵△ABC和△A'B'C'关于MN对称,
∴∠BOM=∠B'OM.
又∵△A'B'C'和△A″B″C″关于EF对称,
∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α
即∠BOB″=2α.
分析:(1)找出△ABC各顶点关于直线MN对称的各对应点,然后顺次连接即可;
(2)作对应点连线的垂直平分线即可求出直线EF;
(3)根据对称找到相等的角,然后进行推理.
点评:解答此题要明确轴对称的性质:
1.对称轴是一条直线.
2.垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线.线段垂直平分线上的点到线段两端的距离相等.
3.在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等.
4.在轴对称图形中,对称轴把图形分成完全相等的两份.
5.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.

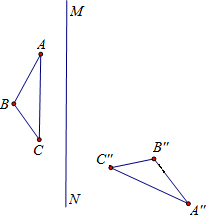 如图:
如图: