Question

证明：对角线相等的菱形是正方形．

Answer 1

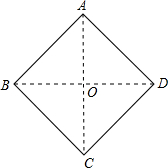
证明：连接AC、BD相交于O
∵菱形ABCD
∴OA=OC=AC，OB=OD=BD
∵AC=BD
∴OA=OB
∵OA⊥OB（菱形的对角线互相垂直）
∴∠OAB=∠OBA=45°
同理∠OBC=∠OCB=45°
∴∠OBA+∠OBC=90°
∴∠ABC=90°
∴ABCD是正方形．
分析：由已知可得ABCD是菱形，则可根据有一个角是直角的菱形是正方形来判定．
点评：本题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念，途经有两种：
①先说明它是矩形，再说明有一组邻边相等；
②先说明它是菱形，再说明它有一个角为直角．