
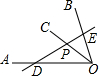
 如图,已知OC是∠AOB的平分线,点P在OC上,且OP=2厘米,∠AOB=60°,过点P的动直线交OA于点D,交OB于E,那么
如图,已知OC是∠AOB的平分线,点P在OC上,且OP=2厘米,∠AOB=60°,过点P的动直线交OA于点D,交OB于E,那么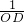
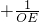 =________厘米.
=________厘米.
 (OD+OE),又S△DOE=
(OD+OE),又S△DOE= OD•OE•sin∠DOE=
OD•OE•sin∠DOE= OD•OE•
OD•OE• ,所以
,所以 (OD+OE)=
(OD+OE)= OD•OE•
OD•OE• ,将等式变形,即可求出
,将等式变形,即可求出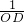 +
+ 的值.
的值. 解:如图,过点P作PM⊥OD于M,PN⊥OE于N,
解:如图,过点P作PM⊥OD于M,PN⊥OE于N, OP=1厘米,
OP=1厘米, OD•PM+
OD•PM+ OE•PN=
OE•PN= (OD+OE),
(OD+OE), OD•OE•sin∠DOE=
OD•OE•sin∠DOE= OD•OE•
OD•OE• ,
, (OD+OE)=
(OD+OE)= OD•OE•
OD•OE• ,
, OD•OE,
OD•OE,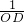 +
+ =
= .
. .
. (OD+OE)=
(OD+OE)= OD•OE•
OD•OE• ,是解题的关键.
,是解题的关键. 

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com