
分析 (1)根据观察函数图象,可得自变量、因变量,根据路程随时间的变化而变化,可得答案;
(2)根据函数图象的纵坐标,可得离家的距离,根据函数图象的横坐标,可得离家的时间;
(3)根据函数图象的纵坐标,可得离家最远距离,根据函数图象的横坐标,可得离家最远时间;
(4)根据函数图象的纵坐标,可得11时、12时离家的距离,根据有理数的减法,可得答案;
(5)根据函数图象的纵坐标,可得离家最远时间,根据函数图象的横坐标,可得返回的时间,根据路程与时间的关系,可得答案.
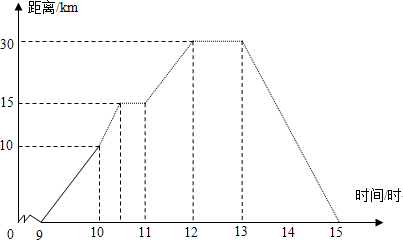
解答 解:(1)图象表示变量 路程 和 时间 的关系; 时间是自变量,路程是因变量,
故答案为:路程;时间;时间;距离;
(2)10时,他距离家 10 km,13时他距离家 30 km,
故答案为:10;30;
(3)他到达离家最远的地方是 12 时,距离 30 km,
故答案为:12,30;
(4)11时到12时他行驶了 15 km,
故答案为:15;
(5)他由离家最远的地方返回的平均速度是30÷(15-13)=15(km/h).
点评 本题考查了函数图象,观察函数图象的纵坐标得出路程,函数图象的横坐标得出时间是解题关键.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
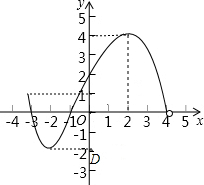 观察图,回答下列问题:
观察图,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com