
如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.
(1)赛道的长度是 m,甲的速度是 m/s;
(2)分别写出甲在 和
和 时,y关于t的函数关系式:
时,y关于t的函数关系式:
当 ,y= ;当
,y= ;当 时,y= ;
时,y= ;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米。
(1) 1)50,2.5; (2)当0≤t≤20时,y=90-2.5t , 当20<t≤40时, y=2.5t-50 .(3)画图见解析;(4)5,40.
解析试题分析:(1)由于甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程,又因为y表示船离开池边B1B2的距离,所以图2中当t=0时对应的y值即为赛道的长度;因为30秒钟甲船从A1处运动到B1处,即20s运动50m,根据速度=路程÷时间,即可求出甲的速度;
(2)先根据图象的形状,可判断出甲船在0≤t≤30和30<t≤60时,y都是t的一次函数,设出其解析式,再运用待定系数法求解;
(3)乙的速度为2m/s,由B2到达A2的路程为赛道的长度50m,根据时间=路程÷速度,即可求出乙船由B2到达A2的时间为25s;乙船在2分钟内可运动2个来回,每25s可从赛道一端运动到另外一端,起点在原点,据此在图2中画出乙船在2分钟内的函数图象;
(4)两个图象的交点个数即为相遇次数.
(1)50,2.5;
(2)当0≤t≤20时,y=90-2.5t , 当20<t≤40时, y=2.5t-50 .
(3)因为赛道的长度为50米,乙的速度为2米/秒,所以乙船由B2到达A2的时间为25秒; 乙在3分钟内的函数图象如图5所示: 
(4)从上图可知甲、乙共相遇5次.40米
考点: 一次函数的应用.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航.渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)
(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.
(2)求渔船和渔政船相遇时,两船与黄岩岛的距离.
(3)在渔政船驶往黄岩岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
“兄弟餐厅”采购员某日到集贸市场采购草鱼,若当天草鱼的采购单价 (元)与采购量
(元)与采购量 (斤)之间的关系如图,且采购单价不低于4元/斤.
(斤)之间的关系如图,且采购单价不低于4元/斤.
(1)直接写出 关于
关于 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(2)若这天他采购草鱼的量不多于20斤,那么这天他采购草鱼最多用去多少钱? 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂有A、B两种不同规格的货车车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元。
(1)设运送这批货物的总费用为 万元,这列货车挂A型车厢
万元,这列货车挂A型车厢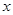 节,试写出
节,试写出 与
与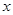 之间的函数关系式;
之间的函数关系式;
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
(3)在上述方案中,哪种方案运费最省,最少运费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
现有一笔直的公路连接M、N两地。甲车从 M 地 驶往 N 地,速度为每小时60km;同时乙车从N地驶往M 地,速度为每小时80 km。途中甲车发生故障,于是停车修理了2.5h,修好后立即开车驶往N地。设乙车行驶的时间为t h,两车之间的距离为S km。已知 S与 t 的函数关系的部分图像如图所示。
(1)求出甲车出发几小时后发生故障。
(2)请指出图中线段 BC 的实际意义;
(3)将S与 t 的函数图像补充完整(需在图中标出相应的数据)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在方格纸中(小正方形的边长为1),反比例函数 与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)①分别写出点A、B的坐标;
②把直线AB向右平移5个单位,再向上平移5个单位,求出平移后直线A′B′的解析式;
(2)若点C在函数 的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人1000元的两家旅行社。经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按7折收费;乙旅行社的优惠条件是:学生、家长都按8折收费。假设这两位家长带领 名学生去旅行,甲、乙旅行社的收费分别为
名学生去旅行,甲、乙旅行社的收费分别为 ,
,
(1)、写出 与
与 的函数关系式。
的函数关系式。
(2)、学生人数在什么情况下,选择甲旅行社更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数y=kx+b(k≠ 0)与反比例函数 (m≠0)的图象有公共点A(1,2),D(a,-1).直线 轴于点N(3,0),与一次函数和反比例 函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2),D(a,-1).直线 轴于点N(3,0),与一次函数和反比例 函数的图象分别交于点B,C.
(1) 求一次函数与反比例函数的解析式;
(2) 求△ABC的面积。
(3) 根据图象回答,在什么范围时,一次函数的值大于反比例函数的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com