解:(1)∵AB=AC,∠A=x°,
∴∠ACB=∠B=

,
又∵CD平分∠ACB,
∴∠ACD=

∠ACB=
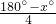
,
∴∠BDC=∠A+∠ACD=x°+
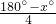
=
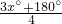
,
∴y=

x+45.
故答案为y=

x+45;
(2)∵∠BCD=

∠ACB=
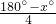
=45°-

x°,∠BDC=

x°+45°,∠DBC=2∠BCD,
∴∠BCD<∠BDC,∠BCD<∠DBC,
∴△BCD中BD边最小.
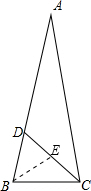
作∠ABC的平分线交CD于E.
∵∠DBE=

∠ABC=

∠ACB=∠DCB,∠BDE=∠CDB,
∴△BDE∽△CDB,
∴BD:CD=BE:BC=DE:BD.(*)
设BE=CE=z,则DE=n+1-z.
下面分两种情况讨论BC与CD的关系:
①当BC>CD时,设BD、CD、BC分别为n,n+1,n+2,再设BE=CE=z,则DE=n+1-z.将它们代入(*),得

=
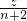
=
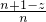
,
由

=
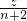
,得z=
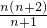
,
由

=
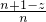
,得n+1-z=
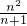
,
两式相加,得n+1=
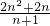
,
解得n=1.
由三角形三边关系定理可知1,2,3不能组成三角形,所以BC>CD不成立;
②当BC<CD时,设BD、BC、CD分别为n,n+1,n+2,再设BE=CE=z,则DE=n+2-z.将它们代入(*),得

=
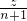
=
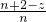
,
由

=
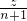
,得z=
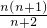
,
由

=
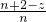
,得n+2-z=
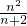
,
两式相加,得n+2=
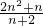
,
解得n
1=4,n
2=-1(不合题意,舍去),
∴BD=4,BC=5,CD=6.
∵CD平分∠ACB,
∴AD:BD=AC:BC,
∴AD:4=AC:5,
设AD=4x,则AC=5x,
∵AB=AC,∴4x+4=5x,∴x=4,
∴AB=AC=20.
在△ABC中,AB=AC=20,BC=5,
由余弦定理,得cosA=

=
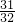
,
∴sinA=
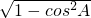
=
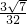
;
(3)△ADC的面积=

×16×20×
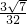
=15

.
分析:(1)先根据三角形内角和定理和角平分线的性质得出∠ACD,再根据三角形的外角性质即可求解;
(2)作∠ABC的平分线交CD于E,则△BDE∽△CDB,根据相似三角形对应边成比例可计算出n=4;
(3)由正弦定理直接求出.
点评:考查了等腰三角形的性质,相似三角形的判定与性质,余弦定理以及正弦定理,综合性较强,属于竞赛题型,难度较大.

 △ABC中,AB=AC,CD平分∠ACB.
△ABC中,AB=AC,CD平分∠ACB. ,
, ∠ACB=
∠ACB=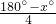 ,
,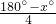 =
=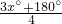 ,
, x+45.
x+45. x+45;
x+45; (2)∵∠BCD=
(2)∵∠BCD= ∠ACB=
∠ACB=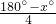 =45°-
=45°- x°,∠BDC=
x°,∠BDC= x°+45°,∠DBC=2∠BCD,
x°+45°,∠DBC=2∠BCD, ∠ABC=
∠ABC= ∠ACB=∠DCB,∠BDE=∠CDB,
∠ACB=∠DCB,∠BDE=∠CDB, =
=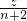 =
=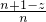 ,
, =
=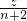 ,得z=
,得z=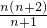 ,
, =
=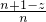 ,得n+1-z=
,得n+1-z=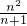 ,
,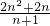 ,
, =
=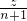 =
=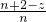 ,
, =
=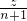 ,得z=
,得z=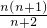 ,
, =
=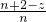 ,得n+2-z=
,得n+2-z=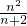 ,
,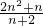 ,
, =
=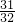 ,
,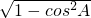 =
=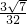 ;
; ×16×20×
×16×20× =15
=15 .
.

 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°, ,连接AO、BE、DC.
,连接AO、BE、DC.