
如图(1),在□ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA。
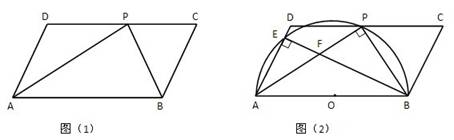
1.判断△APB是什么三角形?证明你的结论;
2.比较DP与PC的大小;
3.如图(2)以AB为直径作半圆O,交AD于点E,连结BE与AP交于点F,若AD=5cm,AP=8cm,求证△AEF∽△APB,并求tan∠AFE的值。
1.△APB是直角三角形,理由如下:
∵ 在□ABCD中,AD∥BC,
∴ ∠DAB +∠ABC = 180°;
又∵AP与BP分别平分∠DAB和∠CBA,
∴∠PAB = ,∠PBA =
,∠PBA =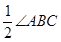 ,
,
∴ ∠PAB+∠PBA= ,
,
∴ △APB是直角三角形;
2.∵ DC∥AB,
∴∠BAP =∠DPA.
∵∠DAP =∠PAB,
∴∠DAP =∠DPA,
∴ DA = DP
同理证得CP=CB.
∴ DP = PC
3.∵AB是⊙O直径,
∴∠AEB = 90°.
又(1)易知∠APB = 90°.
∴ ∠AEB =∠APB,
∵ AP为角平分线,即∠EAF=∠PAB,
∴ △AEF∽△APB,
由(2)可知DP = PC = AD,
∴ AB = DC = 2AD = 10cm,
在Rt△PAB中,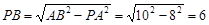 (cm)
(cm)
又△AEF∽△APB,
得∠AFE=∠ABP,
∴ tan∠AFE =
tan∠ABP= 。
。
【解析】
1.可通过角的度数来判断三角形APB的形状.由于ABCD是平行四边形,AD∥BC,那么同旁内角∠DAB和∠CBA的和应该是180°,AP,BE平分∠DAB,∠ABP,于是∠PAB和∠ABP的和就应该是90°,即∠APB=90°,因此可得出三角形APB的形状.
2.可通过平行和角平分线,通过等角对等边得出DP=AP,同理可证出PC=BC,根据平行四边形的性质,AD=BC,可得出DP=PC.
3.利用两个角相等求出△AEF∽△APB,然后利用(2)求出PB的长度,在根据∠AFE=∠ABP,然后求出tan∠AFE的值.


科目:初中数学 来源: 题型:
| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
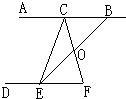 28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.
28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.查看答案和解析>>
科目:初中数学 来源: 题型:
| AE |
| BE |
| ED |
| BE |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com