
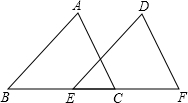
 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )| A. | ∠A=∠D | B. | BC=EF | C. | ∠ACB=∠F | D. | AC=DF |
科目:初中数学 来源: 题型:解答题
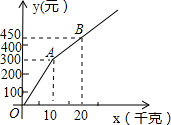 甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
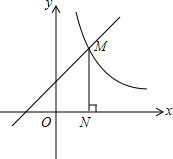 如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1
如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向上,顶点坐标为(-1,-4) | B. | 开口向下,顶点坐标为(1,4) | ||
| C. | 开口向上,顶点坐标为(1,4) | D. | 开口向下,顶点坐标为(-1,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2mn)2=4m2n2 | B. | (-2mn)2=4m2n2 | C. | (2m2n2)3=8m6n6 | D. | (-2m2n2)3=-8m5n5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com