
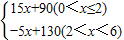
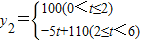 y2=
y2=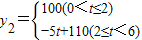 及t=6-x即可求出y2与x的函数关系:当0<x≤4时,y2=5x+80;当4≤x<6时,y2=100;
及t=6-x即可求出y2与x的函数关系:当0<x≤4时,y2=5x+80;当4≤x<6时,y2=100;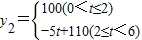 ,
,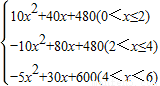 ;
;

 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完.该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售量x(千件)的关系为:
y1=![]()
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为
![]() y2=
y2=
(1)用x的代数式表示t为:t= 6﹣x ;当0<x≤4时,y2与x的函数关系为:y2= 5x+80 ;当 4 <x< 6 时,y2=100;
(2)求每年该公司销售这种健身产品的总利润w(千元)与国内销售数量x(千件)的函数关系式,并指出x的取值范围;
(3)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市南长区九年级上学期期末考试数学试卷(解析版) 题型:解答题
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售数量x(千件)的关系为:y1= 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=
(1)用x的代数式表示t,则t=__________;当0<x≤3时,y2与x的函数关系式为:y2=__________________;当3≤x<________时,y2=100;
(2)当3≤x<6时,求每年该公司销售这种健身产品的总利润w(千元)与国内的销售数量x(千件)的函数关系式,并求此时的最大利润.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏苏州市九年级12月反馈测试数学试卷(解析版) 题型:解答题
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售数量x(千件)的关系为: 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: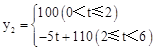
(1)用x的代数式表示t为:t= ;当0<x≤4时, y2与x的函数关系为y2= ;当 ≤x< 时,y2=100;
(2)求每年该公司销售这种健身产品的总利润w(千元)与国内的销售数量x(千件)的函数关系式,并指出x的取值范围;
(3)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖北黄冈卷)数学(解析版) 题型:解答题
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润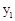 (元)与国内销售数量
(元)与国内销售数量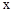 (千件)的关系为:
(千件)的关系为: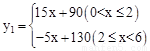 若在国外销售,平均每件产品的利润
若在国外销售,平均每件产品的利润 (元)与国外的销售数量t(千件)的关系为:
(元)与国外的销售数量t(千件)的关系为: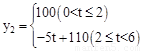
(1)用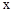 的代数式表示t为:t= ;当0<
的代数式表示t为:t= ;当0<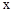 ≤4时,
≤4时,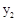 与
与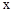 的函数关系式为:
的函数关系式为: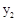 = ;当4≤
= ;当4≤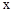 < 时,
< 时,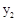 =100;
=100;
(2)求每年该公司销售这种健身产品的总利润W(千元)与国内的销售数量x(千件)的函数关系式,并指出x的取值范围;
(3)该公司每年国内、国外的销量各为多少时,可使公司每年的总利润最大?最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com