Question

已知D是Rt△ABC斜边AB上的中点，∠A=20°，那么∠BCD=________度．

Answer 1

70
分析：如图，连接CD；根据直角三角形斜边上的中线的性质推知等腰三角形ACD的两个底角的度数；然后由图形中的∠ACD+∠BCD=90°即可求得∠BCD的度数．
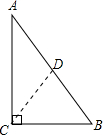
解答：解：如图，连接CD；
∵D是Rt△ABC斜边AB上的中点，
∴AD=CD（直角三角形斜边上的中线等于斜边的一半），
∴∠A=∠ACD；
又∵∠A=20°，∠ACB=90°，
∴∠BCD=∠ACB-∠A=70°；
故答案是：70．
点评：本题考查了直角三角形的斜边上的中线．直角三角形斜边上的中线等于斜边的一半．