
| 1 | 4 |
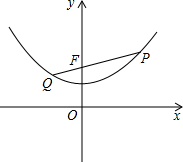 0,2)的距离为d2
0,2)的距离为d2| 1 |
| 4 |
| 1 |
| 4 |
t2+(
|
| 1 |
| 2 |


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
| ||
| 3 |
| 2 |
| 3 |
| 3 |
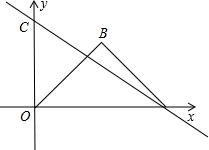 角形,∠B=90°,抛物y=mx2+3x过点B,将△OAB绕点O顺时针旋转,使点B落在直线AC上的点B′处.
角形,∠B=90°,抛物y=mx2+3x过点B,将△OAB绕点O顺时针旋转,使点B落在直线AC上的点B′处.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 48 |
查看答案和解析>>
科目:初中数学 来源:2013届北京市第六十三中学初三第一学期期中考试数学试卷(带解析) 题型:解答题
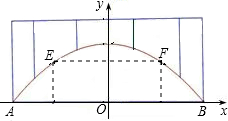
如图,已知抛物线C1: 的顶点为P, 与x轴相交于A、B两点(点A在点B的左侧),点B 的横坐标是1.
的顶点为P, 与x轴相交于A、B两点(点A在点B的左侧),点B 的横坐标是1.
(1)求a的值;
(2)如图,抛物线C2与抛物线C1关于x轴对称,将抛物 线C2向右平移,平移后的抛物线记为C3,抛物线
C3 的顶点为M,当点P、M关于点O成中心对称时,求抛物线C3的解析式.
查看答案和解析>>
科目:初中数学 来源:2009年江苏省南通市中考模拟考试数学试卷(解析版) 题型:解答题
 交两坐标轴于点A、C,△OAB是等腰直角三角形,∠B=90°,抛物y=mx2+3x过点B,将△OAB绕点O顺时针旋转,使点B落在直线AC上的点B′处.
交两坐标轴于点A、C,△OAB是等腰直角三角形,∠B=90°,抛物y=mx2+3x过点B,将△OAB绕点O顺时针旋转,使点B落在直线AC上的点B′处.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市初三第一学期期中考试数学试卷(解析版) 题型:解答题
如图,已知抛物线C1: 的顶点为P,
与x轴相交于A、B两点(点A在点B的左侧),点B 的横坐标是1.
的顶点为P,
与x轴相交于A、B两点(点A在点B的左侧),点B 的横坐标是1.

(1)求a的值;
(2)如图,抛物线C2与抛物线C1关于x轴对称,将抛物 线C2向右平移,平移后的抛物线记为C3,抛物线
C3 的顶点为M,当点P、M关于点O成中心对称时,求抛物线C3的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com