
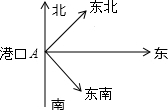
 如图所示,一轮船以8nmile/h的速度从港口A出发向东北方向航行,另一轮船以6nmile/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距多远?
如图所示,一轮船以8nmile/h的速度从港口A出发向东北方向航行,另一轮船以6nmile/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距多远?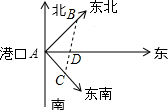 解:∵两船分别沿东北及东南方向行驶,
解:∵两船分别沿东北及东南方向行驶,| AB2+AC2 |
| 162+122 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:044
如图所示,一轮船在海上以每小时30海里的速度向正西方向航行,上午8∶00时,在B处测得小岛A在北偏东![]() 方向;之后轮船继续向正西方向航行,于上午9∶00时到达C处,这时测得小岛A在北偏东
方向;之后轮船继续向正西方向航行,于上午9∶00时到达C处,这时测得小岛A在北偏东![]() 方向;如果轮船继续向正西方向航行,于上午11∶00时到达D处,这时轮船与小岛A相距多远?
方向;如果轮船继续向正西方向航行,于上午11∶00时到达D处,这时轮船与小岛A相距多远?

查看答案和解析>>
科目:初中数学 来源:2012-2013年江苏省张家港市八年级10月月考数学试卷(解析版) 题型:解答题
如图所示,一轮船以8 nmile/h的速度从港口A出发向东北方向航行,另一轮船以6 nmile/h的速度同时从港口出发向东南方向航行,那么离开港口A 2 h后,两船相距多远?

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
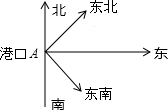 如图所示,一轮船以8nmile/h的速度从港口A出发向东北方向航行,另一轮船以6nmile/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距多远?
如图所示,一轮船以8nmile/h的速度从港口A出发向东北方向航行,另一轮船以6nmile/h的速度同时从港口出发向东南方向航行,那么离开港口A2h后,两船相距多远?查看答案和解析>>
科目:初中数学 来源:2012-2013年江苏省张家港市八年级10月月考数学试卷(带解析) 题型:解答题
如图所示,一轮船以8 nmile/h的速度从港口A出发向东北方向航行,另一轮船以6 nmile/h的速度同时从港口出发向东南方向航行,那么离开港口A 2 h后,两船相距多远?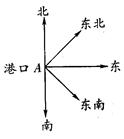
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com