
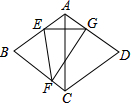
 如图,在菱形ABCD中,∠BAD=120°,点E,F分别在AB,BC上,将△BEF沿EF折叠,点B落在AD上的点G处,EG⊥AC.
如图,在菱形ABCD中,∠BAD=120°,点E,F分别在AB,BC上,将△BEF沿EF折叠,点B落在AD上的点G处,EG⊥AC.分析 (1)根据翻折的性质得出∠BEF=∠GEF,∠BFE=∠GFE,再利用三角形内角和解答即可;
(2)首先证明△ABC,△ADC都是等边三角形,再证明FG是菱形的高,根据2•S△ABC=BC•FG即可解决问题.
解答 解:(1)∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD,∠CAB=∠CAD=60°,
∴△ABC,△ACD是等边三角形,
∵EG⊥AC,
∴∠AEG=∠AGE=30°,
∵∠B=∠EGF=60°,
∵将△BEF沿EF折叠,
∴∠BEF=∠GEF=$\frac{1}{2}(180°-30°)=75°$,
∴∠BFE=∠GFE=180°-60°-75°=45°,
∴∠BFG=90°,
(2)∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD,∠CAB=∠CAD=60°,
∴△ABC,△ACD是等边三角形,
∵EG⊥AC,
∴∠AEG=∠AGE=30°,
∵∠B=∠EGF=60°,
∴∠AGF=90°,
∴FG⊥BC,
∴2•S△ABC=BC•FG,
∴2×$\frac{\sqrt{3}}{4}$×(6$\sqrt{2}$)2=6$\sqrt{2}$•FG,
∴FG=3$\sqrt{6}$,
故答案为:75°;90°.
点评 本题考查菱形的性质、等边三角形的判定和性质、翻折变换、菱形的面积等知识,关键是记住菱形的面积=底×高=对角线乘积的一半.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,-4),直线x=-1 | B. | (1,-4),直线x=1 | C. | (-1,4),直线x=-1 | D. | (1,4),直线x=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一个正方体的表面展开图,每个面上都标注了字母,请根据要求回答下列问题:
如图是一个正方体的表面展开图,每个面上都标注了字母,请根据要求回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?
如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-2 | B. | m>2 | C. | m<-2 | D. | m<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com