
| 5 |
| k |
| x |

| k |
| x |
| 6 |
| x |
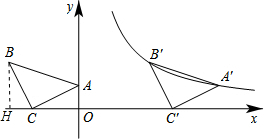 解:(1)过B点作BH⊥x轴于H,如图,
解:(1)过B点作BH⊥x轴于H,如图,| 5 |
| AC2-OC2 |
|
| k |
| x |
| 6 |
| x |


科目:初中数学 来源: 题型:
| -k2-4 |
| x |
| A、y1<y2<y3 |
| B、y1<y3<y2 |
| C、y1>y2>y3 |
| D、y1>y3>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A | B | |
| 每件进价/元 | 1200 | 1000 |
| 每件售价/元 | 1380 | 1200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
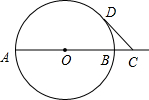 已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 为增强市民的节能意识,我市试行阶梯电价.从2013年开始,按照每户每年的用电量分三个档次计费,具体规定见右图.小明统计了自己2013年前5个月的实际用电量为1300度,请帮助小明分析下面问题.
为增强市民的节能意识,我市试行阶梯电价.从2013年开始,按照每户每年的用电量分三个档次计费,具体规定见右图.小明统计了自己2013年前5个月的实际用电量为1300度,请帮助小明分析下面问题.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com