练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

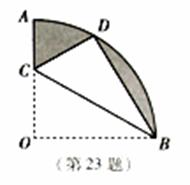
    如图，在扇形中，，半径．将扇形沿过点的直线折叠．点恰好落在上点处，折痕交于点，求整个阴影部分的周长和面积．

     [答案] 周长：；面积：.

    [考点] 图形的折叠：折叠前、后的图形全等；全等三角形的性质：全等三角形对应边相等，全等三角形对应角相等；圆：弧长和扇形面积：弧长，.正三角形的判定：三边相等的三角形是正三角形.正三角形的性质.锐角三角函数：解直角三角形.

    [解析] 如图（第23题），由折叠前、后的图形全等.所以，，，.又在扇形中，，半径．所以，，，的长.所以，

    整个阴影部分的周长的长.

    如图（第23题-1），连接扇形的半径，

    由正三角形，在中，，

    所以，整个阴影部分的面积

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图1，在平面直角坐标系中，抛物线y=
    1
    4
    x2-6    与直线y=
    1
    2
    x    相交于A，B两点．
    （1）求线段AB的长；
    （2）若一个扇形的周长等于（1）中线段AB的长，当扇形的半径取何值时，扇形的面积最大，最大面积是多少；
    （3）如图2，线段AB的垂直平分线分别交x轴、y轴于C，D两点，垂足为点M，分别求出OM，OC，OD的长，并验证等式
    1
    OC2
    +
    1
    OD2
    =
    1
    OM2
    是否成立；
    （4）如图3，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，设BC=a，AC=b，AB=c．CD=b，试说明：
    1
    a2
    +
    1
    b2
    =
    1
    h2
    ．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

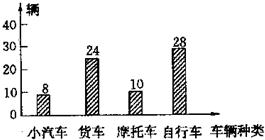    24、小刚站在一个路口观察过往的车辆，统计了半小时内各种车辆通过的数量，并制成了条形统计图（如图所示）．
    （1）请你根据图中的数据，编制一个统计表；
    （2）根据这个条形统计图画出扇形统计图，并在扇形统计图上标明各种不同的车辆占通过的总车辆的百分比；
    （3）你从中得到了什么信息？请简要说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图，在平面直角坐标系中，抛物线与直线相交于两点．

    (1）求线段的长．

    (2）若一个扇形的周长等于（1）中线段的长，当扇形的半径取何值时，扇形的面积最大，最大面积是多少？

    (3）如图2，线段的垂直平分线分别交轴、轴于两点，垂足为点，分别求出的长，并验证等式是否成立．

    　

    (4）如图3，在中，，，垂足为，设，，．，试说明：．

    查看答案和解析>>

    科目：初中数学 来源：101网校同步练习　初三数学　北师大(新课标2001/3年初审) 北师大版 题型：044

    如图，在直角坐标系xOy中，已知菱形OABC的顶点O在坐标原点，顶点B在y轴正半轴上，OA边在直线y＝x上，AB边在直线y＝－x＋上．

    (1)根据题意，直接写出菱形顶点，O、A、B、C的坐标，以及边长和∠AOC的度数；

    (2)在OB上有一动点P，以O为圆心，OP为半径画弧MN，分别交OA、OC于点M、N(M、N可以与A、C重合)，作⊙Q与AB、BC、弧MN都相切．设⊙Q的半径为R，OP的长为y，求y与R之间的函数关系式；

    (3)以O为圆心，OA为半径作扇形OAC，请问在菱形OABC中，除去扇形OAC后的剩余部分内，是否可以作出一个圆，使所得的圆是以扇形OAC为侧面的圆锥的底面，若存在，求出这个圆的面积；若不存在说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2007年广东省深圳市初中毕业生学业考试数学试卷 题型：044

    如图，在平面直角坐标系中，抛物线相交于A，B两点．

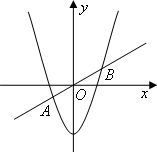
    (1)求线段AB的长．

    (2)若一个扇形的周长等于(1)中线段AB的长，当扇形的半径取何值时，扇形的面积最大，最大面积是多少？

    (3)如图，线段AB的垂直平分线分别交x轴、y轴于C，D两点，垂足为点M，分别求出OM，OC，OD的长，并验证等式是否成立．

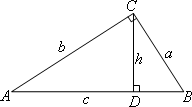
    (4)如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，设BC＝a，AC＝b，AB＝c．CD＝b，试说明：．

    查看答案和解析>>

    同步练习册答案