
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植蜜柚,已知该蜜柚的成本价为8元/千克。
到了收获季节,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
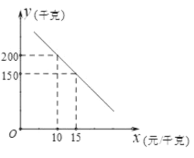
干克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围:
(2)当该蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该蜜柚的保持期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
【答案】(1)y与x的函数关系式为y=-10x+300(8≤x≤30);(2)x=19时,w取得最大值,最大值为1210;(3)不能销售完这批蜜柚.
【解析】
(1)利用待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”列出函数解析式,并配方成顶点式即可得出最大值;
(3)求出在(2)中情况下,即x=19时的销售量,据此求得40天的总销售量,比较即可得出答案.
(1)设y与x的函数关系式为y=kx+b,
将(10,200)、(15,150)代入,得:![]() ,
,
解得:![]() ,
,
∴y与x的函数关系式为y=-10x+300(8≤x≤30);
(2)设每天销售获得的利润为w,
则w=(x-8)y
=(x-8)(-10x+300)
=-10(x-19)2+1210,
∵8≤x≤30,
∴当x=19时,w取得最大值,最大值为1210;
(3)由(2)知,当获得最大利润时,定价为19元/千克,
则每天的销售量为y=-10×19+300=110千克,
∵保质期为40天,
∴总销售量为40×110=4400,
又∵4400<4800,
∴不能销售完这批蜜柚.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
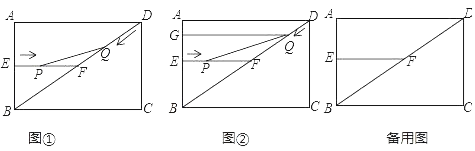
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
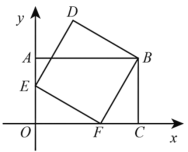
【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0), 则点D的坐标为( )
A. (1, 3)B. (1,![]() )C. (1,
)C. (1,![]() )D. (
)D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是边长为![]() 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
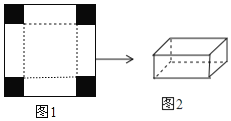
(1)设剪去的小正方形的边长为![]() ,折成的长方体盒子的容积为
,折成的长方体盒子的容积为![]() , 用只含字母
, 用只含字母![]() 的式子表示这个盒子的高为________
的式子表示这个盒子的高为________![]() ,底面积为________
,底面积为________![]() ,盒子的容积
,盒子的容积![]() 为________
为________![]() ;
;
(2)为探究盒子的体积与剪去的小正方形的边长![]() 之间的关系,小明列表
之间的关系,小明列表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
| _______ |
|
|
| _______ |
|
|
请将表中数据补充完整,并根据表格中的数据写出当![]() 的值逐渐增大时,
的值逐渐增大时,![]() 的值如何变化?
的值如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P,Q在数轴上分别表示的数分别为p,q,我们把p,q之差的绝对值叫做点P,Q之间的距离,即![]() .如图,在数轴上,点A,B,O,C,D的位置如图所示,则
.如图,在数轴上,点A,B,O,C,D的位置如图所示,则![]() ;
;![]() ;
;![]() .请探索下列问题:
.请探索下列问题:
![]()
(1)计算![]() ____________,它表示哪两个点之间的距离?________________________.
____________,它表示哪两个点之间的距离?________________________.
(2)点M为数轴上一点,它所表示的数为x,用含x的式子表示PB=____________;当PB=2时,x=____________;当x=____________时,|x+4|+|x-1|+|x-3|的值最小.
(3)|x-1|+|x-2|+|x-3|+…+|x-2018|+|x-2019|的最小值为________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A,B表示到﹣2的距离都为6,P为线段AB上任一点,C,D两点分别从P,B同时向A点移动,且C点运动速度为每秒2个单位长度,D点运动速度为每秒3个单位长度,运动时间为t秒.
![]()
(1)A点表示数为 ,B点表示数为 ,AB= .
(2)若P点表示的数是0,
①运动1秒后,求CD的长度;
②当D在BP上运动时,求线段AC,CD之间的数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里.
7 |
| ﹣3 | ﹣5 | 0 | 2014 | ﹣46 | 7.8 | ﹣1 |
正数集合:{ ……};
负数集合:{ ……};
整数集合:{ ……};
分数集合:{ ……}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小明记录的今年雨季一周河水的水位变化情况(上周末的水位达到警戒水位).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | +0.20 | +0.81 | ﹣0.35 | +0.03 | +0.28 | ﹣0.36 | ﹣0.01 |
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
(2)与上周相比,本周末河流水位是上升了还是下降了?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com