
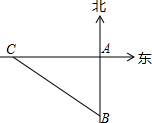
 如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.
如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.分析 (1)作出肯定回答:这艘轮船不改变航向,那么它能进入台风影响区;
(2)首先假设轮船能进入台风影响区,进而利用勾股定理得出等式求出即可;
(3)根据(2)中x的值即可得出结论.
解答 解:(1)根据题意得:轮船不改变航向,轮船会进入台风影响区;
(2)如图所示: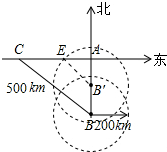
设x小时后,就进入台风影响区,根据题意得出:
CE=30x千米,BB′=20x千米,
∵BC=500km,AB=300km,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{50{0}^{2}-30{0}^{2}}$=400(km),
∴AE=400-30x,AB′=300-20x,
∴AE2+AB′2=EB′2,
即(400-30x)2+(300-20x)2=2002,
解得:x1=$\frac{180-10\sqrt{51}}{13}$≈8.3,x2=$\frac{180+10\sqrt{51}}{13}$≈19.3,
∴轮船经8.3小时就进入台风影响区;
(3)由(2)知,从8.3小时到19.3小时轮船受到台风影响,
∴轮船受台风影响的时间=19.3-8.3=11(小时),
答:轮船受到台风影响一共经历了11小时.
点评 此题主要考查了一元二次方程的应用以及勾股定理等知识;根据题意得出关于x的方程是解决问题的关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC.
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示.线段OB,OC,OA的长度分别是1,2,3.且OC平分∠AOB.若将点A表示为(3,20°),点B表示为(1,110°).则点C可表示为(2,65°).
如图所示.线段OB,OC,OA的长度分别是1,2,3.且OC平分∠AOB.若将点A表示为(3,20°),点B表示为(1,110°).则点C可表示为(2,65°).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com