C
分析:连接PC,由AB为圆P的切线,根据切线的性质得到PC与AB垂直,连接OA,过O作OD垂直于AB,由垂径定理得到D为AB的中点,由OD和PC都与AB垂直,得到OD与PC平行,由OP与AB平行,可得出四边形ODPC为平行四边形,根据平行四边形的对边相等可得OD=PC,又阴影部分的面积用圆O的面积减去圆P的面积,表示出阴影部分的面积,在直角三角形AOD中,利用勾股定理表示出三边的关系,变形后代入表示出的阴影部分面积,再根据阴影部分的面积可得出AD的长,进而确定出AB的长.
解答:连接PC,可得PC⊥AB,再连接OA,过O作OD⊥AB,交AB于点D,如图所示:

∵PC⊥AB,OD⊥AB,
∴∠ODC=∠PCB=90°,
∴PC∥OD,又AB∥OP,
∴四边形OPCD为平行四边形,
∴PC=OD,
又∵OD⊥AB,
∴D为AB的中点,即AD=BD=

AB,
∵在Rt△OAD中,根据勾股定理得:OA
2=OD
2+AD
2,即OA
2-OD
2=AD
2,
且S
阴影=16π,
∴S
阴影=π•OA
2-πPC
2=π•OA
2-πOD
2=π(OA
2-OD
2)=πAD
2=16π,
∴AD
2=16,即AD=4,
则AB=2AD=8.
故选C
点评:此题考查了切线的性质,涉及的知识有:垂径定理,勾股定理,平行四边形的判定与性质,以及阴影部分面积的求法,熟练掌握切线的性质是解本题的关键.

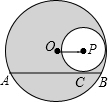 如图,⊙P内含于⊙O,⊙O的弦AB切⊙P于点C,且AB∥OP.若阴影部分的面积为16π,则弦AB的长为
如图,⊙P内含于⊙O,⊙O的弦AB切⊙P于点C,且AB∥OP.若阴影部分的面积为16π,则弦AB的长为
 AB,
AB,

 名校课堂系列答案
名校课堂系列答案