
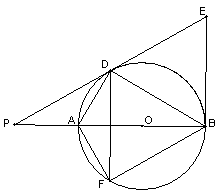
如图,![]() 是圆
是圆![]() 的直径,
的直径,![]() 为圆心,
为圆心,![]() 、
、![]() 是半圆的弦,且
是半圆的弦,且![]() . 延长
. 延长![]() 交圆的切线
交圆的切线![]() 于点
于点![]()
(1) 判断直线![]() 是否为
是否为![]() 的切线,并说明理由;
的切线,并说明理由;
(2) 如果![]() ,
,![]() ,求
,求![]() 的长。
的长。
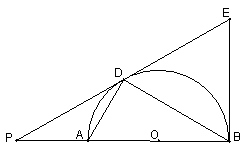
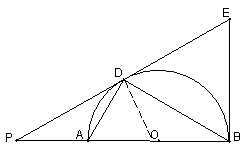
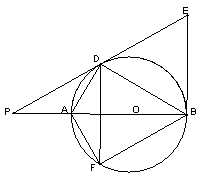
 (3)将线段
(3)将线段![]() 以直线
以直线![]() 为对称轴作对称线段
为对称轴作对称线段![]() ,点
,点![]() 正好在圆
正好在圆![]() 上,如图2,求证:四边形
上,如图2,求证:四边形![]() 为菱形
为菱形
解:(1)直线![]() 为⊙O的切线 …………1分
为⊙O的切线 …………1分
证明:连结OD ∵![]() 是圆
是圆![]() 的直径 ∴∠ADB=90° …………2分
的直径 ∴∠ADB=90° …………2分
∴∠ADO+∠BDO=90° 又∵DO=BO ∴∠BDO=∠PBD
 ∵
∵![]() ∴∠BDO=∠PDA …………3分
∴∠BDO=∠PDA …………3分
∴∠ADO+∠PDA=90° 即PD⊥OD …………4分
∵点D在⊙O上,
∴直线![]() 为⊙O的切线. …………5分
为⊙O的切线. …………5分
(2)解:∵ BE是⊙O的切线 ∴∠EBA=90°
∵![]() ∴∠P=30° …………6分
∴∠P=30° …………6分
∵![]() 为⊙O的切线 ∴∠PDO=90°
为⊙O的切线 ∴∠PDO=90°
在RT△PDO中,∠P=30°![]() ∴
∴![]() 解得OD=1 …………7分
解得OD=1 …………7分
 ∴
∴![]() …………8分
…………8分
∴PA=PO-AO=2-1=1 …………9分
(3)(方法一)证明:依题意得:∠ADF=∠PDA ∠PAD=∠DAF
∵![]() ∠ADF=∠ABF
∠ADF=∠ABF
∴∠ADF=∠PDA=∠PBD=∠ABF …………10分
∵![]() 是圆
是圆![]() 的直径 ∴∠ADB=90°
的直径 ∴∠ADB=90°
设∠PBD=![]() ,则∠DAF=∠PAD=
,则∠DAF=∠PAD=![]() ,∠DBF=
,∠DBF=![]()
∵四边形AFBD内接于⊙O ∴∠DAF+∠D![]() BF=180°
BF=180°
即 ![]() 解得
解得![]()
∴∠ADF=∠PDA=∠PBD=∠ABF=30° …………11分
∵ BE、ED是⊙O的切线 ∴DE=BE ∠EBA=90°
∴∠DBE=60°∴△BDE是等边三角形。∴BD=DE=BE …………12分
又∵∠FDB=∠ADB—∠ADF =90°-30°=60° ∠DBF=![]() =60°
=60°
∴△BDF是等边三角形。 ∴BD=DF=BF …………13分
∴DE=BE=DF=BF ∴四边形![]() 为菱形 …………14分
为菱形 …………14分
 (方法二)证明:依题意得:∠ADF=∠PDA ∠APD=∠AFD
(方法二)证明:依题意得:∠ADF=∠PDA ∠APD=∠AFD
∵![]() ∠ADF=∠ABF ∠PAD=∠DAF
∠ADF=∠ABF ∠PAD=∠DAF
∴∠ADF=∠AFD=∠BPD=∠ABF …………10分
∴ AD=AF BF//PD …………11分
∴ DF⊥PB ∵ BE为切线 ∴ BE⊥PB ∴ DF//BE………12分
∴四边形![]() 为平行四边形…………13分
为平行四边形…………13分
∵ PE 、BE为切线 ∴ BE=DE
∴四边形![]() 为菱形 …………14分
为菱形 …………14分


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源:2010年中考数学复习课堂练习-直线与圆的位置关系 题型:013
如图AB是⊙O的直径,AC是⊙O的切线,,A为切点,连结BC交圆0于点D,连结AD,若∠ABC=45°,则下列结论正确的是
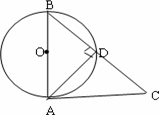
AD=![]() BC
BC
AD=![]() AC
AC
AC>AB
AD>DC
查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初三数学 华东师大(新课标2001/3年初审) 华东师大版 题型:044
如图AB是⊙O的直径,点C是BA延长线上一点,点D在⊙O上,弦DE//CB,Q为AB上一动点,CA=OA=OB=a,CD是⊙O半径的![]() 倍.
倍.

(1)猜想CD与⊙O的位置关系并证明你的猜想.
(2)当Q从A向B运动的过程中,圆中阴影部分的面积是否发生变化,若发生变化请说明你的理由,若不发生变化,请求出阴影部分面积(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源:2009年湖南省邵阳市毕业学业水平考试数学试题 题型:013
如图AB是⊙O的直径,AC是⊙O的切线,,A为切点,连结BC交圆0于点D,连结AD,若∠ABC=450,则下列结论正确的是.
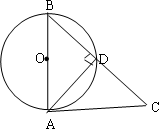
A.![]()
B.![]()
C.AC>AB
D.AD>DC
查看答案和解析>>
科目:初中数学 来源: 题型:
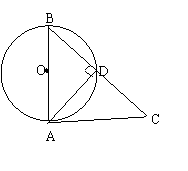
如图AB是⊙O的直径,AC是⊙O的切线,,A为切点,连结BC交圆0于点D,连结AD,若∠ABC=45![]() ,则下列结论正确的是 . ( )
,则下列结论正确的是 . ( )
A.AD=![]() BC B.AD=
BC B.AD=![]() AC C.AC>AB D.AD>DC
AC C.AC>AB D.AD>DC
 |
查看答案和解析>>
科目:初中数学 来源:同步题 题型:单选题

 BC
BC AC
AC 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com