Question

已知∠AOB=30°，P为∠AOB内部一点，点P关于OA、OB的对称点分别为P₁、P₂，则△OP₁P₂是________．

Answer 1

等边三角形
分析：根据轴对称的性质，∠AOB=30°，P为∠AOB内部一点，点P关于OA、OB的对称点分别为P₁、P₂，∠AOP=∠AOP₁，∠BOP=∠BOP₂，可求出∠P₁OP₂的度数，确定三角形的形状．
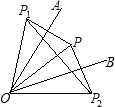
解答：解：连接OP，
∵P₁与P关于OA对称，
∴OP=OP₁，
∵P₂与P关于OB对称，
∴OP=OP₂，
∴OP₁=OP₂①，
∵P₁与P关于OA对称，
∴∠POA=∠AOP₁，
∵P₂与P关于OB对称，
∴∠BOP=∠BOP₂，
又∵∠P₁OP₂=∠AOP₁+∠AOP+∠BOP+∠BOP₂，
∵∠P₁OP₂=∠BOP+∠BOP+∠AOP+∠AOP，
=2（∠BOP+∠APO），
=2∠AOB，
∵∠AOB=30°，
∵∠P₁OP₂=2×30°=60° ②，
由①、②得
△OP₁P₂为等边三角形（有一个角是60的等腰三角形是等边三角形）．
点评：本题考查轴对称的性质，对应点的连线与对称轴的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．