
(本小题满分12分)如图, 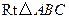 内接于
内接于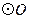 ,
,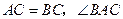 的平分线
的平分线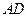 与
与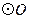 交于点
交于点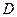 ,与
,与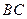 交于点
交于点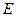 ,延长
,延长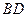 ,与
,与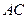 的延长线交于点
的延长线交于点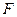 ,连接
,连接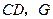 是
是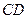 的中点,连结
的中点,连结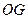 .
.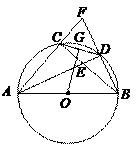
(1)判断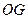 与
与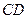 的位置关系,写出你的结论并证明;
的位置关系,写出你的结论并证明;
(2)求证: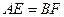 ;
;
(3)若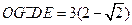 ,求
,求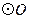 的面积.
的面积.
(1)猜想: .
.
证明:如图,连结OC、OD.
∵ ,G是CD的中点,
,G是CD的中点,
∴由等腰三角形的性质,有 .
.
(2)证明:∵AB是⊙O的直径,∴∠ACB=90°.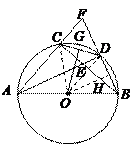 而∠CAE=∠CBF(同弧所对的圆周角相等).
而∠CAE=∠CBF(同弧所对的圆周角相等).
在Rt△ACE和Rt△BCF中,
∵∠ACE=∠BCF=90°,AC=BC,∠CAE=∠CBF,
∴Rt△ACE≌Rt△BCF (ASA)
∴ .
.
(3)解:如图,过点O作BD的垂线,垂足为H.则H为BD的中点.
∴OH=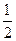 AD,即AD=2OH.
AD,即AD=2OH.
又∠CAD=∠BAD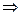 CD=BD,∴OH=OG.
CD=BD,∴OH=OG.
在Rt△BDE和Rt△ADB中,
∵∠DBE=∠DAC=∠BAD,
∴Rt△BDE∽Rt△ADB
∴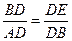 ,即
,即
∴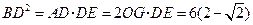
又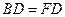 ,∴
,∴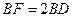 .
.
∴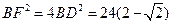 … ①
… ①
设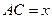 ,则
,则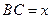 ,AB=
,AB= .
.
∵AD是∠BAC的平分线,
∴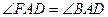 .
.
在Rt△ABD和Rt△AFD中,
∵∠ADB=∠ADF=90°,AD=AD,∠FAD=∠BAD,
∴Rt△ABD≌Rt△AFD(ASA).
∴AF=AB= ,BD=FD.
,BD=FD.
∴CF=AF-AC=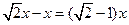
在Rt△BCF中,由勾股定理,得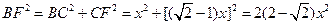 …②
…②
由①、②,得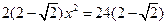 .
.
∴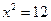 .解得
.解得 或
或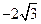 (舍去).
(舍去).
∴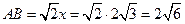
∴⊙O的半径长为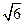 .
.
∴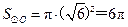
解析


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
(本小题满分12分)如图所示,在梯形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() 与
与![]() 相切于
相切于![]() .已知
.已知![]() ,边
,边![]() 比
比![]() 大6.
大6.

(1)求边 、
、 的长.
的长.
(2)在直径 上是否存在一动点
上是否存在一动点 ,使以
,使以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出
相似?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
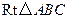 内接于
内接于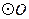 ,
,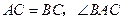 的平分线
的平分线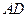 与
与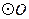 交于点
交于点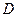 ,与
,与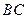 交于点
交于点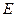 ,延长
,延长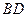 ,与
,与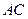 的延长线交于点
的延长线交于点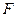 ,连接
,连接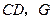 是
是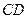 的中点,连结
的中点,连结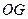 .
.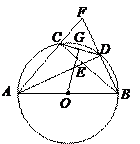
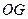 与
与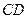 的位置关系,写出你的结论并证明;
的位置关系,写出你的结论并证明;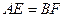 ;
;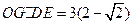 ,求
,求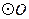 的面积.
的面积.查看答案和解析>>
科目:初中数学 来源: 题型:

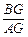 的值.
的值.查看答案和解析>>
科目:初中数学 来源: 题型:
 中,
中, ,
, ,以
,以 为直径的
为直径的 与
与 相切于
相切于 .已知
.已知 ,边
,边 比
比 大6.
大6.
 、
、 的长.
的长. 上是否存在一动点
上是否存在一动点 ,使以
,使以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出
相似?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
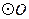 的直径
的直径 和
和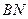 是它的两条切线,
是它的两条切线,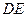 切
切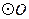 于E,交AM于D,交BN于C.设
于E,交AM于D,交BN于C.设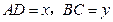 .
.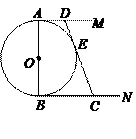
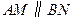 ;
;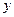 关于
关于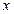 的关系式;
的关系式;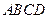 的面积S,并证明:
的面积S,并证明: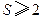 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com