
 的图象上一点,AB⊥x轴的正半轴于B点,C是OB的中点;一次函数y2=ax+b的图象经过A、C两点,并将y轴于点D(0,-2),若S△AOD=4.
的图象上一点,AB⊥x轴的正半轴于B点,C是OB的中点;一次函数y2=ax+b的图象经过A、C两点,并将y轴于点D(0,-2),若S△AOD=4.
 解:(1)作AE⊥y轴于E,
解:(1)作AE⊥y轴于E, OD•AE=4
OD•AE=4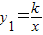 中,得k=8,
中,得k=8,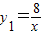 ,(3分)
,(3分)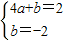 解之得:
解之得: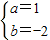


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源:2010年浙江省杭州市十三中中考数学模拟试卷(3月份)(解析版) 题型:解答题
 的图象上一点,AB⊥x轴的正半轴于B点,C是OB的中点;一次函数y2=ax+b的图象经过A、C两点,并将y轴于点D(0,-2),若S△AOD=4.
的图象上一点,AB⊥x轴的正半轴于B点,C是OB的中点;一次函数y2=ax+b的图象经过A、C两点,并将y轴于点D(0,-2),若S△AOD=4.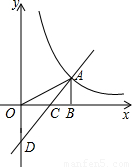
查看答案和解析>>
科目:初中数学 来源:2009年湖北省襄樊市中考数学试卷(解析版) 题型:解答题
 的图象上一点,AB⊥x轴的正半轴于B点,C是OB的中点;一次函数y2=ax+b的图象经过A、C两点,并将y轴于点D(0,-2),若S△AOD=4.
的图象上一点,AB⊥x轴的正半轴于B点,C是OB的中点;一次函数y2=ax+b的图象经过A、C两点,并将y轴于点D(0,-2),若S△AOD=4.
查看答案和解析>>
科目:初中数学 来源:2010年湖南省邵阳市邵东县省示范高中自主招生数学试卷(解析版) 题型:解答题
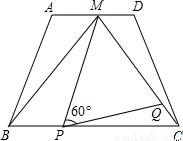 (2009•襄阳)如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
(2009•襄阳)如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.查看答案和解析>>
科目:初中数学 来源:2009年湖北省襄樊市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com