
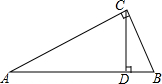
 如图所示,CD是Rt△ABC的斜边AB上的高.
如图所示,CD是Rt△ABC的斜边AB上的高.分析 (1)由在Rt△ABC中,CD是斜边AB上的高,可得∠ACB=∠ADC=∠CDB=90°,又由公共角相等,证得△ACD∽△ABC,△CBD∽△ABC,则可得△ACD∽△CBD∽△ABC;
(2)根据△ACD∽△CBD,从而得出$\frac{AD}{CD}=\frac{CD}{BD}$,于是得出答案;
(3)根据△CBD∽△ABC,从而得出CB2=AB.BD,于是得出答案.
解答 解:(1)∵在Rt△ABC中,CD是斜边AB上的高,
∴∠ACB=∠ADC=∠CDB=90°,
∵∠A=∠A,∠B=∠B,
∴△ACD∽△ABC,△CBD∽△ABC,
∴△ACD∽△CBD∽△ABC,
∴图中有3对相似三角形;
(2)∴△ADC∽△CDB,
∴$\frac{AD}{CD}=\frac{CD}{BD}$,
∴$\frac{9}{6}=\frac{6}{BD}$,
解得:CD=4;
(3)∵△CBD∽△ABC,
∴$\frac{BC}{AB}=\frac{BD}{BC}$,
∴$\frac{15}{25}=\frac{BD}{15}$,
解得:BD=9.
点评 本题考查了相似三角形的判定及性质,利用三角形相似,找到线段比.从而求出线段的长度.这是相似三角形中求线段的长常用的方法.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
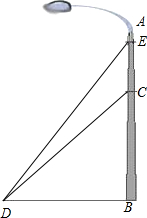 一灯柱AB被一钢缆CD固定,CD与地面成45°夹角,且BD=5m,现再在C点上方2m处加固另一根钢缆ED,那么钢缆ED的长度为多少?(结果保留根号)
一灯柱AB被一钢缆CD固定,CD与地面成45°夹角,且BD=5m,现再在C点上方2m处加固另一根钢缆ED,那么钢缆ED的长度为多少?(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com