
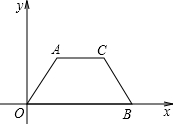
 如图所示,梯形AOBC中,AC∥OB,AO=CB,A(2,2
如图所示,梯形AOBC中,AC∥OB,AO=CB,A(2,2 ),B(8,0),O(0,0).
),B(8,0),O(0,0).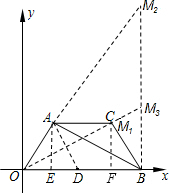
 ),
), ,
, );
); OB=4=AC.
OB=4=AC. OB.
OB.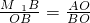 ,
, );
);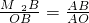 ,
, ,
, ,
, );
);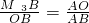 ,
, ,
, )
) )或(8,8
)或(8,8 )或(8,
)或(8, )
) OB,则可得点A在⊙D上;∠OAB=90°.即△OAB是直角三角形.故符合题意的点M有以下3种情况:;①当△OM1B与△BAO相似时(如图),则有
OB,则可得点A在⊙D上;∠OAB=90°.即△OAB是直角三角形.故符合题意的点M有以下3种情况:;①当△OM1B与△BAO相似时(如图),则有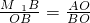 ,②当△OM2B与△OBA相似时,即过B点作OB的垂线交OA的延长线于M2(如图),则有
,②当△OM2B与△OBA相似时,即过B点作OB的垂线交OA的延长线于M2(如图),则有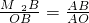 ③当△OM3B与△BOA相似时,即过B点作OB的垂线交OC的延长线于M3(如图),则有
③当△OM3B与△BOA相似时,即过B点作OB的垂线交OC的延长线于M3(如图),则有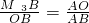 代入数值依次求解即可.
代入数值依次求解即可.

科目:初中数学 来源:新课程学习手册 数学 八年级(下) 配人教课标版 题型:013
如图所示,梯形ABCD中,AB∥CD,对角线AC,BD相交于O,下面四个结论:①△AOB∽△COD
②△AOD∽△BOC
③S△DOC∶S△BOA=DC∶AB
④S△AOD=S△BOC
其中结论始终正确的有

A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源:同步单元练习 八年级数学下 题型:022
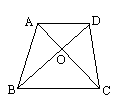
如图所示,梯形ABCD中,AD∥BC,AC、BD相交于点O.若S△AOD∶S△COB=1∶9,则S△AOB∶S△AOD=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com