
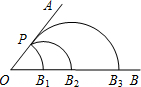
 如图,点P为射线OA上一点,以点O为圆心,线段OP为半径画弧交OB于点B1,接着以点B1为圆心,线段PB1为半径画弧交OB于点B2,再以点B2为圆心,线段PB2为半径画弧交OB于点B3,构成一幅“海螺”图案,若∠AOB=52°,则弧PB3的度数是( )
如图,点P为射线OA上一点,以点O为圆心,线段OP为半径画弧交OB于点B1,接着以点B1为圆心,线段PB1为半径画弧交OB于点B2,再以点B2为圆心,线段PB2为半径画弧交OB于点B3,构成一幅“海螺”图案,若∠AOB=52°,则弧PB3的度数是( )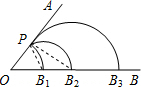 解:如图,连接PB1、PB2,
解:如图,连接PB1、PB2,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 如图,点A在射线OP上,OA等于2cm.我们定义如下两种操作
如图,点A在射线OP上,OA等于2cm.我们定义如下两种操作查看答案和解析>>
科目:初中数学 来源: 题型:
 9、如图,点A在射线OB上,OA的长为2cm.如果OA绕点O按逆时针方向旋转30°到OA',那么点A'的位置可以用(2,30°)表示.按上述表示方法,如果将OA'再绕点O按逆时针方向继续旋转25°到OA″,那么点A″的位置可以用(
9、如图,点A在射线OB上,OA的长为2cm.如果OA绕点O按逆时针方向旋转30°到OA',那么点A'的位置可以用(2,30°)表示.按上述表示方法,如果将OA'再绕点O按逆时针方向继续旋转25°到OA″,那么点A″的位置可以用(
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com