
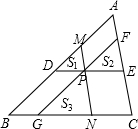
 如图,DE∥BC,FG∥AB,MN∥AC,且DE、FG、MN交于点P.若记S△ABC=S,S△PDM=S1,S△PEF=S2,S△PGN=S3.请猜想:S与S1、S2、S3之间存在怎样的关系?你能加以验证吗?
如图,DE∥BC,FG∥AB,MN∥AC,且DE、FG、MN交于点P.若记S△ABC=S,S△PDM=S1,S△PEF=S2,S△PGN=S3.请猜想:S与S1、S2、S3之间存在怎样的关系?你能加以验证吗? +
+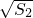 +
+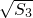 =
= .
. =
=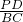 ,
, =
= ,
, =
= ,
, +
+ +
+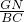 =
=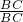 =1
=1 =
=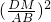 ,
, =
= ,
,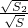 =
= ,
, =
=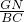 ,
, +
+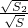 +
+ =1,
=1, +
+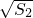 +
+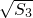 =
= .
. =
= ,
, =
= ,进一步得出
,进一步得出 +
+ +
+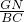 =
=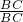 =1,再利用相似三角形面积比是相似比的平方即可得出结论.
=1,再利用相似三角形面积比是相似比的平方即可得出结论. +
+ +
+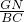 =
=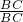 =1,这是此题的突破点,此题属于难题.
=1,这是此题的突破点,此题属于难题. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com