
 如图,在平面直角坐标系xOy中,E(8,0),F(0,6).
如图,在平面直角坐标系xOy中,E(8,0),F(0,6).分析 (1)利用各点坐标进而得出△FQG∽△GRE,求出对应角相等,进而得出答案;
(2)利用网格结合已知得出当P点坐标为(7,7)时,符合题意.
解答 解:(1)∵E(8,0),F(0,6).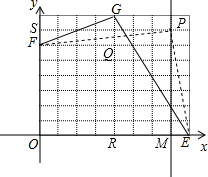
当G(4,8)时,
∴FQ=4,GQ=2,GR=8,RE=4,
∴$\frac{FQ}{GR}$=$\frac{GQ}{ER}$=$\frac{1}{2}$,
又∵∠FQG=∠GRE=90°,
∴△FQG∽△GRE,
∴∠FGQ=∠REG,∠GFQ=∠RQE,
∴∠FGQ+∠RGE=90°,
∴∠FGE=90°,
故答案为:90;
(2)如图所示:P (7,7),PM是分割线;
故答案为(7,7).
点评 此题主要考查了应用设计与作图以及相似三角形的判定与性质,借助网格得出线段长度是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小强骑自行车去郊游,如图表示他离家的距离y(千米)与所用时间x(小时)之间变化关系的图象,小强9点离开家,根据这个图象,请你回答下列问题:
小强骑自行车去郊游,如图表示他离家的距离y(千米)与所用时间x(小时)之间变化关系的图象,小强9点离开家,根据这个图象,请你回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象在第一、三象限 | B. | 图象经过(2,1) | ||
| C. | 在每个象限中,y随x的增大而减小 | D. | 当x>1时,-2<y<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
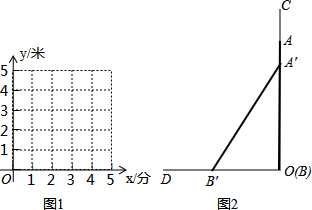
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com