Question

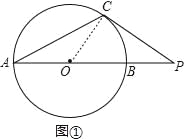
【题目】在⊙O中，AB为直径，C为⊙O上一点．

（1）如图1，过点C作⊙O的切线，与AB延长线相交于点P，若∠CAB=27°，求∠P的度数；

（2）如图2，D为弧AB上一点，OD⊥AC，垂足为E，连接DC并延长，与AB的延长线交于点P，若∠CAB=10°，求∠P的大小．

Answer 1

【答案】（1）∠P =36°；（2）∠P=30°．

【解析】

试题（Ⅰ）连接OC，首先根据切线的性质得到∠OCP=90°，利用∠CAB=27°得到∠COB=2∠CAB=54°，然后利用直角三角形两锐角互余即可求得答案；

（Ⅱ）根据E为AC的中点得到OD⊥AC，从而求得∠AOE=90°﹣∠EAO=80°，然后利用圆周角定理求得∠ACD=∠AOD=40°，最后利用三角形的外角的性质求解即可．

试题解析：（Ⅰ）如图，连接OC，

∵⊙O与PC相切于点C，

∴OC⊥PC，即∠OCP=90°，

∵∠CAB=27°，

∴∠COB=2∠CAB=54°，

在Rt△AOE中，∠P+∠COP=90°，

∴∠P=90°﹣∠COP=36°；

（Ⅱ）∵E为AC的中点，

∴OD⊥AC，即∠AEO=90°，

在Rt△AOE中，由∠EAO=10°，

得∠AOE=90°﹣∠EAO=80°，

∴∠ACD=∠AOD=40°，

∵∠ACD是△ACP的一个外角，

∴∠P=∠ACD﹣∠A=40°﹣10°=30°．