
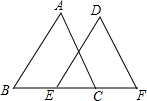
 将△ABC沿直线BC平移,得到△DEF(如图).求证:
将△ABC沿直线BC平移,得到△DEF(如图).求证: 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
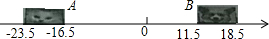 七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:
七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
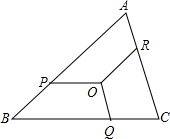 如图,点O是△ABC内一点,点P、Q、R分别在边AB、BC、CA上,且OP∥BC,OQ∥CA,OR∥AB,OP=OQ=OR,BC=a,CA=b,AB=c,求OP的长.
如图,点O是△ABC内一点,点P、Q、R分别在边AB、BC、CA上,且OP∥BC,OQ∥CA,OR∥AB,OP=OQ=OR,BC=a,CA=b,AB=c,求OP的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{y}$=$\frac{2}{3}$ | B. | x=2,y=3,z=4 | C. | 2x=3y | D. | $\frac{x+y+z}{9}$=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,PA、PB是⊙O的切线,CD切⊙O于E,PA=6,∠APB=60°.求:
如图,PA、PB是⊙O的切线,CD切⊙O于E,PA=6,∠APB=60°.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
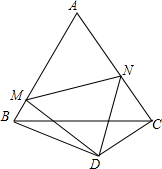 已知,如图,△ABC是等边三角形,BD=DC,∠BDC=120°,∠MDN=60°,求证:C△AMN=$\frac{2}{3}$•C△ABC.(提示:先证:MN=BM+NC)
已知,如图,△ABC是等边三角形,BD=DC,∠BDC=120°,∠MDN=60°,求证:C△AMN=$\frac{2}{3}$•C△ABC.(提示:先证:MN=BM+NC)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com