
如图,抛物线 与直线
与直线 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为 。点P是y轴右侧的抛物线上一动点,过点P作
。点P是y轴右侧的抛物线上一动点,过点P作 轴于点E,交CD于点F.
轴于点E,交CD于点F.

(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由。
(3)若存在点P,使 ,请直接写出相应的点P的坐标
,请直接写出相应的点P的坐标
(1)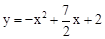 ;(2)当m=1或2或
;(2)当m=1或2或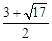 时,以O,C,P,F为顶点的四边形是平行四边形,理由见解析;(3)P(
时,以O,C,P,F为顶点的四边形是平行四边形,理由见解析;(3)P( )或(
)或(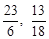 ).
).
【解析】
试题分析:(1)由直线 经过点C,求出点C的坐标;由抛物线
经过点C,求出点C的坐标;由抛物线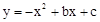 经过点C,D两点,用待定系数法即可求出抛物线的解析式;(2)因为PF∥CO,所以当PF=CO时,以O,C,P,F为顶点的四边形是平行四边形,分
经过点C,D两点,用待定系数法即可求出抛物线的解析式;(2)因为PF∥CO,所以当PF=CO时,以O,C,P,F为顶点的四边形是平行四边形,分 和
和 两种情况讨论即可;(3)如图,当点P在CD上方且∠PCF=450时,作PM⊥CD于点M,CN⊥PF于点N,则△PMF∽△CNF,∴
两种情况讨论即可;(3)如图,当点P在CD上方且∠PCF=450时,作PM⊥CD于点M,CN⊥PF于点N,则△PMF∽△CNF,∴ ,∴PM=CM=2CF,∴
,∴PM=CM=2CF,∴ ,又∵
,又∵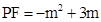 ,∴
,∴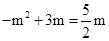 ,解得:
,解得: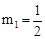 ,
,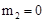 (舍去),∴P(
(舍去),∴P( ),当点P在CD下方且∠PCF=450时,同理可以求得:另外一点为P(
),当点P在CD下方且∠PCF=450时,同理可以求得:另外一点为P(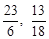 ).
).

试题解析:(1)∵直线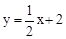 经过点C,∴C(0,2).
经过点C,∴C(0,2).
∵抛物线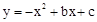 经过点C(0,2),D
经过点C(0,2),D 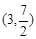 ,
,
∴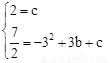 ,解得
,解得 .
.
∴抛物线的解析式为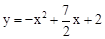 .
.
(2)∵点P的横坐标为m且在抛物线上, ∴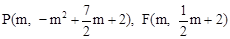 .
.
∵PF∥CO,∴当PF=CO时,以O,C,P,F为顶点的四边形是平行四边形.
当 时,
时, ,
,
∴ ,解得:
,解得: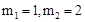 .
.
即当m=1或2时,四边形OCPF是平行四边形.
当 时,
时,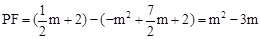 ,
,
∴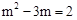 ,解得:
,解得: (∵点P在y轴右侧的抛物线上,∴舍去).
(∵点P在y轴右侧的抛物线上,∴舍去).
即当 时,四边形OCFP是平行四边形.
时,四边形OCFP是平行四边形.
综上所述,当m=1或2或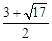 时,以O,C,P,F为顶点的四边形是平行四边形.
时,以O,C,P,F为顶点的四边形是平行四边形.
(3)P( )或(
)或(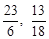 ).
).
考点:1.二次函数综合题;2.单动点问题;3.曲线上点的坐标与方程的关系;4.平行四边形的性质;5.相似三角形的判定和性质;6.分类思想的应用.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
 =-1,与x轴交于点C,且∠ABC=90°
=-1,与x轴交于点C,且∠ABC=90°查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江新世纪外国语学校九年级上学期第一次学力检测数学试卷(解析版) 题型:解答题
如图,抛物线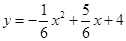 与直线
与直线 交于点A 、B,与y轴交于点C.
交于点A 、B,与y轴交于点C.
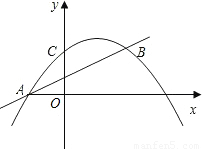
(1)求点A、B的坐标;
(2)若点P是直线x=1上一点,是否存在△PAB是等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(河南卷)数学(解析版) 题型:解答题
如图,抛物线 与直线
与直线 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为 。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
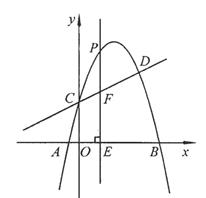
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由;
(3)若存在点P,使∠PCF=450,请直接写出相应的点P的坐标。
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京师大附中九年级第一学期期中考试数学卷 题型:解答题
已知:如图,抛物线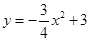 与
与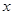 轴交于点
轴交于点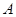 ,点
,点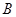 ,与直线
,与直线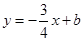 相交于点
相交于点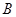 ,点
,点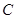 ,直线
,直线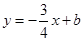 与
与 轴交于点
轴交于点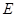 .
.
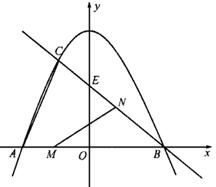
1.(1)求 的面积.
的面积.
2.(2)若点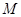 在线段
在线段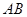 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从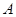 向
向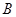 运动(不与
运动(不与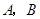 重合),同时,点
重合),同时,点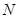 在射线
在射线 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从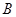 向
向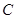 运动.设运动时间为
运动.设运动时间为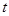 秒,请写出
秒,请写出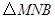 的面积
的面积 与
与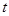 的函数关系式,并求出点
的函数关系式,并求出点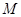 运动多少时间时,
运动多少时间时,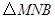 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com