Question

如图：抛物线顶点坐标为点C（1，4），交x轴于点A（3，0），交y轴于点B．
（1）求抛物线和直线AB的解析式；
（2）点Q（x，0）是x轴上的一动点，过Q点作x轴的垂线，交抛物线于P点、交直线BA于D点，连接OD，PB，当点Q（x，0）在x轴上运动时，求PD与x之间的函数关系式；以O、B、P、D为顶点的四边形能否成为平行四边形？若能求出Q点坐标；若不能，请说明理由．
（3）是否存在一点Q，使以PD为直径的圆与y轴相切？若存在，求出Q点的坐标；若不存在，请说明理由．

Answer 1

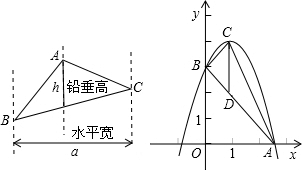
解：（1）设抛物线的解析式为：y₁=a（x-1）²+4，
把A（3，0）代入解析式求得a=-1，
∴y₁=-（x-1）²+4=-x²+2x+3，
设直线AB的解析式为：y₂=kx+b，
由y₁=-x²+2x+3求得B点的坐标为（0，3），
把A（3，0），B（0，3）代入y₂=kx+b中，
解得：k=-1，b=3；
∴直线AB的解析式为：y₂=-x+3；

（2）设存在符合条件的点Q（x，0），则P点、D点的横坐标都为x，
PD=QP-QD=y₁-y₂=（-x²+2x+3）-（-x+3）=-x²+3x，
当PD=OB=3时，四边形OBPD成为平行四边形-x²+3x=3，此方程无解，
∴不存在点Q；
当Q在x轴的负半轴Q′上时，如图：P′D′=（-x+3）-（-x²+2x+3）=x²-3x=OB=3，
解得：x=＞0（舍去），x=，
∴以O、B、P、D为顶点的四边形能成为平行四边形；

（3）假设存在一点Q，使以PD为直径的圆与y轴相切，
①当0＜x＜3时，设半径r，r=PD，PD=QP-QD=y₁-y₂=（-x²+2x+3）-（-x+3）=-x²+3x，
∴r=（-x²+3x），
∴x=（-x²+3x），
解得：x₁=1，x₂=0（舍去），
∴Q₁（1，0）；
①当x＜0时，设半径为r，r=PD，PD=QD-QP=y₂-y₁=（-x+3）-（-x²+2x+3）=x²-3x，
∴r=（x²-3x），
∴-x=（x²-3x），
解得：x₁=1（舍去），x₂=0（舍去），
③当x＞3时，设半径为r，r=PD，PD=QD-QP=y₂-y₁=（-x+3）-（-x²+2x+3）=x²-3x，
∴r=（x²-3x），
∴x=（x²-3x），
解得：x₁=5，x₂=0（舍去），
∴Q₂（5，0）；
∴Q₁（1，0）、Q₂（5，0）时都与y轴相切．
分析：（1）先通过代入A点坐到二次函数解析式中，求出系数a的值，从而求二次函数解析式，再代入A，B求出直线AB解析式；
（2）设高Q（x，0），利用平行四边形性质对边相等列出关于x的方程，注意平行于y轴的直线中，两点之间的线段长度可以有两点的纵坐标之差来求；
（3）利用运动的观点，分别从当0＜x＜3时，x＜0时，x＞3时三类情况讨论圆与y的相切的关系即可求得Q的坐标．
点评：此题考查了待定系数法求二次函数的解析式，平行四边形的判定与性质以及圆的切线的判定与性质等知识．此题综合性很强，注意利用平行于y轴的直线中，两点之间的线段长度可以有两点的纵坐标之差来求是解此题的关键，还要注意数形结合思想与分类讨论思想的应用．