Question

9．在平面直角坐标系内，点O为坐标原点，直线y=$\frac{1}{2}$x+3交x轴于点A，交y轴于点B，点C在x轴正半轴上，△ABC的面积为15．

（1）求直线BC的解析式；
（2）横坐标为t的点P在直线AB上，设d=OP²，求d与t之间的函数关系式．（不必写出自变量取值范围）
（3）在（2）的条件下，当∠BPO=$\frac{1}{2}$∠BCA时，求t的值．

Answer 1

分析 （1）先求出点A，B坐标，用△ABC的面积为15，求出点C的坐标，用待定系数法求出直线BC解析式；
（2）在Rt△OPD中，有OP²=OD²+PD²，代入化简 得d=$\frac{5}{4}$t²+3t+9，
（3）先判断出∠EBA=∠OBA，再分两种情况，①点P在第一象限，用PD=OD建立方程求出t，②当点P位于如图2所示P₁位置时，用P₁O=PO，建立方程求解即可．

解答 解：直线y=$\frac{1}{2}$x+3交x轴于点A，交y轴于点B，
当x=0时y=3，当y=0时，x=-6，
∴A（-6，0）B（0，3），
∴OA=6，OB=3，
∴S_△ABC=$\frac{1}{2}$AC×OB=$\frac{1}{2}$（OA+OC）×OB．
∴15=$\frac{1}{2}$（6+OC）×3
∴OC=4，
∴C（4，0），
设直线BC的解析式为 y=kx+b，
则：$\left\{\begin{array}{l}{3=b}\\{0=4k+b}\end{array}\right.$
∴k=$\frac{3}{4}$
∴直线BC的解析式为y=-$\frac{3}{4}$x+3．
（2）横坐标为t的点P在直线AB上，
∴P（t，$\frac{1}{2}$t+3）
过点P作x轴的垂线，点D为垂足，如图1，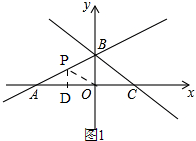

∴D（t，0）
在Rt△OPD中，有OP²=OD²+PD²
∴d=t²+（$\frac{1}{2}$t+3）²=$\frac{5}{4}$t²+3t+9，
（3）在在Rt△OBC内有BC²=OB²+OC²
∴BC=$\sqrt{{3}^{2}+{4}^{2}}$=5
过点A作BC的垂线，点E为垂足，如图2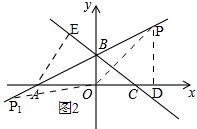

S_△ABC=$\frac{1}{2}$BC•AE=15，
∴AE=6
∴AO=AE，
∵∠AEB=∠AOB=90°
∴∠EBA=∠OBA     
当点P位于第一象限时，
∠BOP=∠ABO-∠APO=$\frac{1}{2}$∠EBO-$\frac{1}{2}$∠BCO=$\frac{1}{2}$（∠EBO-∠BCO）=$\frac{1}{2}$∠BOC=45°  
∴∠POD=∠PDO=45°，
∴PD=OD，
∴$\frac{1}{2}$t+3=t，
∴t=6     
当点P位于如图2所示P₁位置时，
∠BP₁O=$\frac{1}{2}$∠BCA=∠BPO
∴P₁O=PO，
∴P₁O²=PO²，
∴$\frac{5}{4}$t²+3t+9=$\frac{5}{4}$×6²+3×6+9，
解得：t=-$\frac{42}{5}$或t=6（舍去）
综上所述：当∠BPO=$\frac{1}{2}$∠BCA时t的值为6或-$\frac{42}{5}$．

点评 此题是一次函数综合题，主要考查了三角形的面积公式，待定系数法，等腰三角形的性质，解本题的关键是判断出∠EBA=∠OBA，用方程的思想解决问题是解本题的难点．