Question

在△ABC中，∠ACB＝90°，∠CAB＝30°，△ABD是等边三角形

(1)如图，E是AB的中点，连结CE并延长交AD于F．

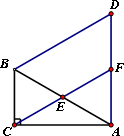
求证：①△AEF≌△BEC；②四边形BCFD是平行四边形；

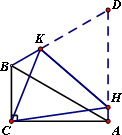
(2)如图，将四边形ACBD折叠，使D与C重合，HK为折痕，求sin∠ACH的值．

Answer 1

答案：
解析：

解：(1)①在△ABC中，∠ACB＝90°，∠CAB＝30°，∴∠ABC＝60°． 　　在等边△ABD中，∠BAD＝60°，∴∠BAD＝∠ABC＝60°． 　　∵E为AB的中点，∴AE＝BE． 　　又∵∠AEF＝∠BEC，∴△AEF≌△BEC　3分 　　②在△ABC中，∠ACB＝90°，E为AB的中点 　　∴CE＝AB，BE＝AB，∴∠BCE＝∠EBC＝60°． 　　又∵△AEF≌△BEC，∴∠AFE＝∠BCE＝60°． 　　又∵∠D＝60°，∴∠AFE＝∠D＝60° 　　∴FC∥BD 　　又∵∠BAD＝∠ABC＝60°，∴AD∥BC，即FD∥BC 　　∴四边形BCFD是平行四边形．　3分 　　(2)∵∠BAD＝60°，∠CAB＝30° 　　∴∠CAH＝90° 　　在Rt△ABC中，∠CAB＝30°，设BC＝a 　　∴AB＝2BC＝2a，∴AD＝AB＝2a． 　　设AH＝x，则 HC＝HD＝AD－AH＝2a－x． 　　在Rt△ABC中，AC2＝(2a)2－a2＝3a2． 　　在Rt△ACH中，AH2＋AC2＝HC2，即x2＋3a2＝(2a－x)2． 　　解得x＝a，即AH＝a． 　　∴HC＝2a－x＝2a－a＝a 　　　4分