
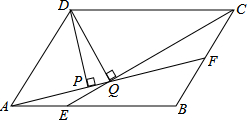
 (2013•无锡)如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )
(2013•无锡)如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 13 |
| 3 |
 解:连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
解:连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
(3a+
|
| 13 |
(3a)2+(
|
| 3 |
| 13 |
| 3 |
| 3 |
| 13 |


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com