解:(1)∵A(4,0),
∴OA=4,
∴等边三角形ABC的高就为2

,
∴B(2,-2

).
设直线BD的解析式为y=kx+b,由题意,得

,

解得:

,
∴直线BD的解析式为:y=

x-

;
(2)作BE⊥x轴于E,
∴∠AEB=90°.
∵以AB为半径的⊙S与y轴相切于点C,
∴BC⊥y轴.
∴∠OCB=90°
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ACO=30°,
∴AC=2OA.
∵A(4,0),
∴OA=4,
∴AC=8,
∴由勾股定理得:OC=4

.
作BE⊥x轴于E,
∴AE=4,
∴OE=8,

∴B(8,-4

);
(3)如图3,以点B为圆心,AB为半径作⊙B,交y轴于点C、E,过点B作BF⊥CE于F,连接AE.
∵△ABC是等边三角形,
∴AC=BC=AB,∠ABC=∠ACB=∠BAC=60°,
∴∠OEA=

∠ABC=30°,
∴AE=2OA.
∵A(4,0),
∴OA=4,
∴AE=8.
在Rt△AOE中,由勾股定理,得
OE=4

.
∵C(0,
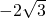
),
∴OC=2

,
在Rt△AOC中,由勾股定理,得
AC=2

.
∵CE=OE-OC=4

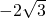
=2

.
∵BF⊥CE,
∴CF=

CE=

,
∴OF=2

+

=3

.
在Rt△CFB中,由勾股定理,得
BF
2=BC
2-CF
2,
=28--3=25,
∴BF=5,
∴B(5,-3

).
过点B作BQ⊥x轴于点Q,
∴BQ=3

,OQ=5,
∴DQ=5,
∴tan∠ODB=

=
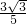
.
分析:(1)先根据等边三角形的性质求出B点的坐标,直接运用待定系数法就可以求出直线BD的解析式;
(2)作BE⊥x轴于E,就可以得出∠AEB=90°,由圆的切线的性质就可以而出B的纵坐标,由直角三角形的性质就可以求出B点的横坐标,从而得出结论;
(3)以点B为圆心,AB为半径作⊙B,交y轴于点C、E,过点B作BF⊥CE于F,连接AE.根据等边三角形的性质圆心角与圆周角之间的关系及勾股定理就可以点B的坐标,作BQ⊥x轴于点Q,根据正切值的意义就可以求出结论.
点评:本题考查了等边三角形的性质的运用,勾股定理的运用,待定系数法求一次函数的解析式的运用,圆周角与圆心角的关系定理的运用,切线的性质的运用及直角三角形的性质的运用,解答时灵活运用勾股定理求线段的值是关键.

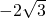 )时,求∠ODB的正切值.
)时,求∠ODB的正切值.
 ,
, ).
). ,
,
 ,
, x-
x- ;
; .
.
 );
); ∠ABC=30°,
∠ABC=30°, .
.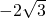 ),
), ,
, .
.
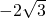 =2
=2 .
. CE=
CE= ,
, +
+ =3
=3 .
. ).
). ,OQ=5,
,OQ=5, =
=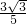 .
.

 金博士一点全通系列答案
金博士一点全通系列答案 如图,△ABC是等边三角形,
如图,△ABC是等边三角形,