
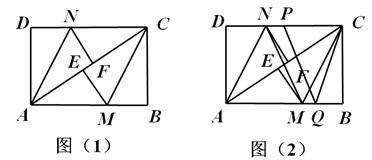
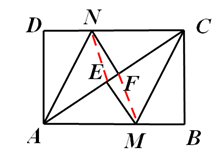
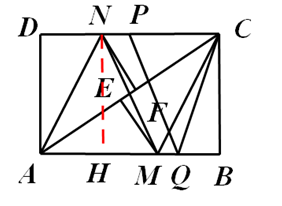
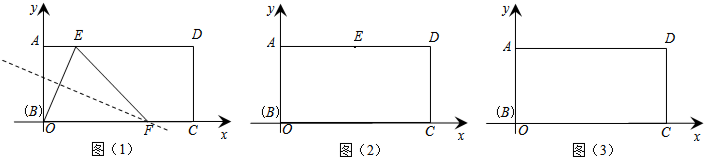
| (1 )证明:∵四边形ABCD 是矩形, ∴∠D= ∠B ,AD=BC ,AD ∥BC , ∴∠DAC= ∠BCA, 又由翻折的性质,得∠DAN= ∠NAF ,∠ECM= ∠BCM , ∴∠DAN= ∠BCM ; ∴△AND≌△CBM(ASA)。 (2 )证明:∵△AND ≌△CBM , ∴DN=BM , 又由翻折的性质,得DN=FN,BM=EM, ∴FN=EM。 又∠NFA=∠ACD+∠CNF=∠BAC+∠EMA=∠MEC, ∴FN∥EM。 ∴四边形MFNE是平行四边形。四边形MFNE 不是菱形,理由如下: 由翻折的性质,得∠CEM= ∠B=900, ∴在△EMF中,∠FEM>∠EFM。 ∴FM>EM, ∴四边形MFNE不是菱形; (3)解:∵AB=4 ,BC=3 , ∴AC=5 。 设DN=x ,则由S△ADC=S△AND+S△NAC 得3 x+5 x=12, 解得x= 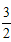 ,即DN=BM= ,即DN=BM=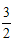 , ,过点N作NH⊥AB于H,则HM=4-3=1, 在△NHM中,NH=3,HM=1, 由勾股定理,得NM= 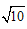 , ,∵PQ∥MN,DC∥AB, ∴四边形NMQP是平行四边形, ∴NP=MQ,PQ= NM= 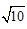 , ,又∵PQ=CQ, ∴CQ= 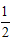 , ,在△CBQ中,CQ= 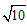 ,CB=3, ,CB=3,由勾股定理,得BQ=1, ∴NP=MQ=  , ,∴PC=4- 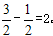 |
  |


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
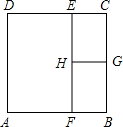 如图,E、F分别在矩形ABCD的边CD、AB上,EF⊥AB,G、H分别是BC、EF的中点,EH>HG,除矩形EFBC外,图中4个矩形都彼此相似,若BC=1,则AB等于( )
如图,E、F分别在矩形ABCD的边CD、AB上,EF⊥AB,G、H分别是BC、EF的中点,EH>HG,除矩形EFBC外,图中4个矩形都彼此相似,若BC=1,则AB等于( )A、
| ||||
B、1+
| ||||
C、
| ||||
D、1+
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
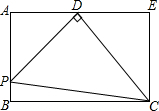 如图,已知:在矩形ABCE中,点D是线段AE上的一个点,AB=3,AD=2,连接CD,过点D作PD⊥CD,交AB于点P.
如图,已知:在矩形ABCE中,点D是线段AE上的一个点,AB=3,AD=2,连接CD,过点D作PD⊥CD,交AB于点P.| PD | CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com