
【题目】如图,过⊙O外一点P作⊙O的两条切线,切点分别为A、B,点M是劣弧AB上的任一点,过M作⊙0的切线分别交PA、PB于点C、D,过圆心O且垂直于OP的直线与PA、PB分别交于点E、F,那么![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
【答案】A
【解析】连接OA、OB、OC、OD、OM,
∵PA、PB、CD都是⊙O的切线,
∴∠OPE=∠OPF,∠OCA=∠OCD,∠ODM=∠ODB,∠OAC=∠OMC=∠OMD=∠OBD=90°,
∴∠COA=∠COM,∠DOM=∠DOB,
∵PO⊥EF,
∴∠POE=∠POF=90°,
又∵PO=PO,
∴△POE≌△POF
∴∠E=∠F,OE=OF.
∵∠E+∠AOE=90°,∠F+∠FOB=90°,
∴∠AOE=∠FOB,
∵∠AOE+∠AOC+∠COM+∠DOM+∠DOB+∠FOB=180°,
∴2∠FOB+2∠AOC+2∠DOB=180°,
∴∠FOB+∠AOC+∠DOB=90°,
∴∠AOC+∠DOF=90°,
又∵∠AOC+∠ACO=90°,
∴∠ACO=∠DOF,
又∵∠E=∠F,
∴△EOC∽△FDO,
∴EC:FO=EO:FD,
∴EC·FD=FO·EO=EO2=![]() EF2,
EF2,
∴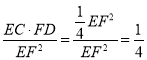 .
.

故选A.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A(-2,1),B(-4,-2),C(-1,-3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′______,B′______;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
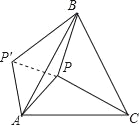
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别骑自行车和摩托车,从同一地点沿相同的路线前往距离80km的某地,图中l1,l2分别表示甲、乙两人离开出发地的距离s(km)与行驶时间t(h)之间的函数关系.请根据图象解答下列问题:
(1)甲、乙两人谁到达目的地较早?早多长时间?
(2)分别求甲、乙两人行驶过程中s与t的函数关系式;
(3)试确定当两辆车都在行驶途中(不包括出发地和目的地)时,t的取值范围;并在这一时间段内,求t为何值时,摩托车行驶在自行车前面?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在![]() 中,
中,![]() ,
,![]() .
.
(1)按下列步骤用尺规作图(保留作图痕迹,不写出作法):作![]() 的平分线AD,交BC于D;
的平分线AD,交BC于D;
(2)在(1)中,过点D作![]() ,交AB于点E,若CD=4,则BC的长为 .
,交AB于点E,若CD=4,则BC的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是![]() .
.
(1)求暗箱中红球的个数;
(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,![]() ,
,![]() ,
,![]() 是三个格点(即小正方形的顶点),判断
是三个格点(即小正方形的顶点),判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;

(2)如图②,连接三格和两格的对角线,求![]() 的度数(要求:画出示意图,并写出证明过程).
的度数(要求:画出示意图,并写出证明过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:①当
的四个命题:①当![]() 时,
时, ![]() 有最小值10;②
有最小值10;②![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于![]() 时的函数值;③若
时的函数值;③若![]() ,且
,且![]() 是整数,当
是整数,当![]() 时,
时, ![]() 的整数值有
的整数值有![]() 个;④若函数图象过点
个;④若函数图象过点![]() 和
和![]() ,其中
,其中![]() ,
, ![]() ,则
,则![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com