
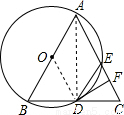
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.DF⊥AC于点F.
(1)求证:DF是⊙O的切线.
(2)当∠B的度数是多少时,DE∥AB?并说明理由.

(1)证明见解析;(2)∠B=60°,理由见解析.
【解析】
试题分析:(1)连接AD、OD,根据圆周角定理求出AD⊥BC,求出BD=DC,推出OD∥AC,求出OD⊥DF,根据切线的判定推出即可;
(2)得出等边三角形ABC,求出∠BAC=60°,根据圆内接四边形的性质求出∠CED=60°,即可得出答案.
(1)证明:连接OD、AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=DC,
∵OA=OB,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线;
(2)【解析】
当∠B=60°时,DE∥AB,
理由是:∵∠B=60°,AC=AB,
∴△ABC是等边三角形,
∴∠BAC=60°,
∵A、E、D、B四点共圆,
∴∠CED=∠ABC=60°,
∴∠CED=∠CAB,
∴DE∥AB.
考点:1.切线的判定;2.等边三角形的判定与性质.


科目:初中数学 来源:2013-2014学年湖南省长沙市长郡教育集团九年级期末考试数学试卷(解析版) 题型:解答题
某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量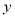 (件)与销售单价
(件)与销售单价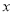 (元)的关系可以近似的看作一次函数(如图).
(元)的关系可以近似的看作一次函数(如图).
(1)求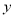 与
与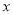 之间的函数关系式;
之间的函数关系式;
(2)设公司获得的总利润(总利润 总销售额
总销售额 总成本)为
总成本)为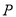 元,求
元,求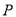 与
与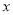 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量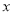 的取值范围;根据题意判断:当
的取值范围;根据题意判断:当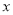 取何值时,
取何值时,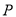 的值最大?最大值是多少?
的值最大?最大值是多少?
(3)若公司要保证利润不能低于4000元,则销售单价x的取值范围为多少元(可借助二次函数的图像解答)?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市长郡教育集团九年级期末考试数学试卷(解析版) 题型:选择题
下列长度的三条线段,能组成三角形的是( )
A.1、l、2 B.3、4、5 C.1、4、6 D.2、3、7
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:解答题
某市自来水公司为了鼓励市民节约用水,于2014年4月开始采用以用户为单位按月分段收费办法收取水费,新按月分段收费标准如下:
标准一:每月用水不超过20吨(包括20吨)的水量,每吨收费2.45元;
标准二:每月用水超过20吨但不超过30吨的水量,按每吨 元收费;
元收费;
标准三:超过30吨的部分,按每吨( +1.62)元收费。(说明:
+1.62)元收费。(说明: >2.45).
>2.45).
(1)居民甲4月份用水25吨,交水费65.4元,求 的值;
的值;
(2) 若居民甲2014年4月以后,每月用水 (吨),应交水费
(吨),应交水费 (元),求
(元),求 与
与 之间的函数关系式,并注明自变量x的取值范围;
之间的函数关系式,并注明自变量x的取值范围;
(3)随着夏天的到来,各家的用水量在不但增加.为了节省开支,居民甲计划自家6月份的水费不能超过家庭月收入的2%(居民甲家的月收入为6540元),则居民甲家六月份最多能用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com